Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TK
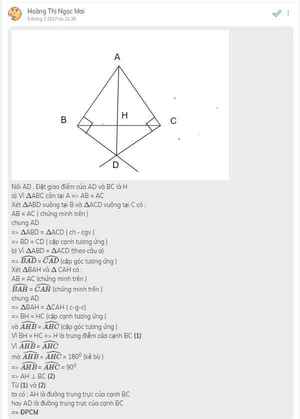
Nguồn: Cho tam giác ABC cân tại A. Qua B kẻ đường thẳng vuông góc vs AB, qua C kẻ đường thẳng vuông góc vsAC, 2 đường thẳng cắt nhau ở D, chứng minh: a, BD=CD B,Đường thẳng AD là dường trung trực của BC - Hoc24

Ta có:
Tam giác ABC cân tại A => góc ABC = góc ACB
Mà góc ABD = góc ACD (=90độ) => góc ABD - góc ABC = góc ACD - góc ACB <=> góc DBC = góc DCB
=> Tam giác DBC cân ở D => DB=DC
b. gỌI I là giao điểm của AD và BC
Ta có: tam giác ABD = tam giác ACD (c-c-c)
=> góc BAD = góc CAD <=> góc BAI = góc CAI
=> tam giác BAI = tam giác CAI (c-g-c) => BI=IC
=> AI là trung trực của BC
CMTT có: DI là trung trực BC
=> Đường thẳng AD là trung trực của BC

B A C D
Xét tam giác ABD và tam giác ACD
có AD chung
góc ABD=góc ACD=90 độ
AB=AC ( Vì tam giác ABC cân tại A)
suy ra tam giác ABD =tam giác ACD (cạnh huyền-cạnh góc vuông)
suy ra BD=CD (hai cạnh tương ứng)

Xét tam giác ADB và tam giác ACD
có AB=AC (tam giác ABC cân tại A)
AD chung
góc ABD = góc ACD = 90độ
suy ra tam giác ADB = tam giác ACD (cạnh huyền-cạnh góc vuông)
suy ra BD=DC (hai cạnh tương ứng) (1)
b) Từ (1) suy ra D thuộc đường trung trực của BC (2)
mà tam giác ABC cân tại A suy ra AB=AC suy ra A thuộc đường trung trực của BC (3)
Từ (2) và (3) suy ra AD là đường TT của BC
???
đề đúng mà