Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) EF là đường trung bình của tam giác ABH => EF//AB; EF=1/2AB (1)
Có G là trung điểm của DC => GC//AB(DC//AB); GC=1/2AB(DC=AB) (2)
Từ (1)$(2) => EF//GC; EF=GC => Tứ giác EFCG là hình bình hành.
b) Xét tam giác EBH và tam giác CBH có:BH là cạnh chung
EHB=CHB=90 (gt)
EH=EC(H là trung điểm của EC)
Vậy tam giác EBH=tam giac CBH (cgv-cgv)
=>BEH=BCH ; EBH=CBH
Lại có:BEH+EBH+BCH+CBH=180 =>BEH=EBH=BCH=CBH=180/4=45 (3)
Co BCE+ECG=BCG
Ma BCG=90(ABCD là hcn); BCE=45(cmt)
=> ECG=45
Xét tam giác EGC có:EGC+GEC+ECG=180
=> EGC=180-(GEC+ECG)
=180-(90+45)=45 (4)
Tu (3)$(4) => BEG=90
c)Tu CM

a, Chú ý EF là đường trung bình trong tam giác HAB
b, Chứng minh F là trực tâm tam giác BEC và sử dụng a)
c, Sử dụng tỉ số sinA trong tam giác vuông HAB và tỉ số tanA trong tam giác vuông BAC để tính AB, CB và AC, EC

1: Xét ΔHAB có
E là trung điểm của HA
F là trung điểm của HB
Do đó: EF là đường trung bình
=>EF//AB và EF=AB/2
hay EF//CD và EF=CD/2
mà G là trung điểm của CD
nên EF=CG và EF//CG
=>EFCG là hình bình hành

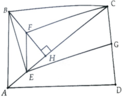
D A B C H E G F hình mk vẽ chưa chuẩn nha vẽ khó lắm.
a; xét tam giác HAB có E và F lần lượt là trung điểm của AH và HB
\(\Rightarrow\) EF là đường trung bình của tam giác HAB
Nên EF \(//\) AB và EF = \(\frac{AB}{2}\) (1)
Mà ABCD là hình chữ nhật nên AB // DC và = DC (2)
Từ (1) và (2) \(\Rightarrow\) EF //DC và = \(\frac{DC}{2}\)
Mà G là trung điểm DC
Nên EF // GC VÀ EF =GC
Do đó TỨ GIÁC EFCG là hình bình hành (tứ giác có 1 cặp cạnh đối // và =)
b;vì BH vuông góc với AC mà F thuộc BH(F là trung điểm BH)
Nên FH vuông góc với AC hay FH vuông góc EC (E thuộc AC)
Suy ra FH là đương cao của tam giác cân FEC (EF =FC T t/c hình bình hành)
nên FH đồng thời là đường trung tuyến EC
Hay BH là đường trung tuyến của EC (F thuộc BH)
MÀ BH là đường cao (GT)
\(\Rightarrow\) BEC là tam giác cân ở B
nên góc BEC = góc BCE ( t/c) (3)
mà góc GEC + góc BEC = BEG(4)
và góc GCE +BCE = BCG =90 Độ (ABCD là hcn)(5)
mà EG =GC (EFCG là hbh) nên tam giác GEC cân ở G (6)
do đó góc GEC= góc GCE(7)
Từ (3);(4);(5);(6)và (7) suy ra góc BCG= BEC =90 độ
c; xét tam giác ABH vuông ở H có ( GÓC BHA =90độ)
sinBAH=\(\frac{BH}{AB}\)\(\Rightarrow\)AB=\(\frac{BH}{sinBAH}\)=\(\frac{4}{sin30}\)=8
xét tam giác ABC vuông ở B (gócABC=90độ)có
BC=AB.tanBAC=8.tan30=\(\frac{8\sqrt{3}}{3}\)
vì ABCD là hcn nên\(S_{ABCD}=AB.BC\)=\(8.\frac{8\sqrt{3}}{3}\)=\(\frac{64\sqrt{3}}{3}\)(đơn vị diện tích)