Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

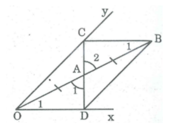
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.

Bài giải:
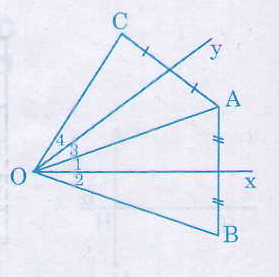
a) Ox là đường trung trực của AB nên OA = OB.
Oy là đường trung trực của AC nên OA = OC.
Suy ra OB = OC.
b) ∆AOB cân tại O (vì OA = OB).
Suy ra ˆO1O1^= ˆO2O2^= 12ˆAOB12AOB^
∆AOC cân tại O (vì OA = OC)
Suy ra ˆO3O3^= ˆO4O4^= 12ˆAOC12AOC^
Do đó ˆAOBAOB^ +ˆAOCAOC^ = 2(ˆO1O1^+ˆO3O3^)
= 2ˆxOyxOy^
= 2.500
=1000
Vậy ˆBOCBOC^ = 1000

Thông báo thay trang thay mặt người phân phối chương trình xin tặng chương trình học online số 1 Việt Nam. Sự kiện bắt đầu từ ngày 28/10 đến 1/11
Xin chào các thành viên đang online trên trang. Sự kiện khuyến mãi được tài trợ 500 suất áo chiếc áo đá bóng Việt Nam.Mong tất cả mọi người đã xem vào truy cập sau để nhận thưởng khi xem có 1 bản đăng kí nhận miễn phí : Thời gian có hạn tặng mọi người đã tham gia tích cực -> Không tin các bạn có thể hỏi các CTV nha mình chỉ có quyền thông báo :
Copy cái này hoặc gõ :
https://lazi.vn/quiz/d/16491/nhac-edm-la-loai-nhac-the-loai-gi
Đúng

B đối xứng với A qua tia 0X. Chọn H làm giao điểm của AB với 0X. Theo tính chất đường tròn.
Ta có: AB vông góc với tia 0X. H là trung điểm của AB.
Suy ra:
AH=HB
0A=0B (1)
C đối xứng với A qua tia 0Y. Chọn K làm giao điểm của AC với 0Y. Theo tính chất đường tròn.
Ta có: AC vông góc với tia 0Y. K là trung điểm của AC.
Suy ra:
AK=KC
0A=0C (2)
Từ (1) và (2), ta có:
0A=0B=0C.
Vậy kết luận 0B=0C.
Vì A đối xứng qua OX nên góc X0A= góc X0B.(3)
Vì A đối xứng qua OY nên góc Y0A= góc Y0C.(4)
Mà góc X0A+A0Y=X0Y.
Theo (3) và (4), ta có:
B0C=2X0A+2A0Y. Hoặc B0C=2XOY.
ta có tam giác AOC và AOB là các tam giác cân, do đó các đường Õ và Oy vừa là đường cao vừa là đường phân giác của 2 tam giác.
⇒[COyˆ=yOAˆAOxˆ= xOBˆ⇒[COy^=yOA^AOx^= xOB^ (1)
để B đối xứng với C qua O thì COAˆ+AOBˆ=180oCOA^+AOB^=180o
đồng thời : COyˆ+yOAˆ=COAˆAOxˆ+ xOBˆ=AOBˆCOy^+yOA^=COA^AOx^+ xOB^=AOB^
⇒COyˆ+yOAˆ+xOAˆ+xOBˆ=COAˆ+AOBˆ=1800⇒COy^+yOA^+xOA^+xOB^=COA^+AOB^=1800 (2)
từ (1) và (2) ⇒2yOAˆ+2 xOAˆ=1800⇔yOAˆ+xOAˆ=900⇒2yOA^+2 xOA^=1800⇔yOA^+xOA^=900
hay xOyˆ=90oxOy^=90o
vậy khi xOyˆ=90oxOy^=90o thì B đối xứng với C qua O

