Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải chi tiết:
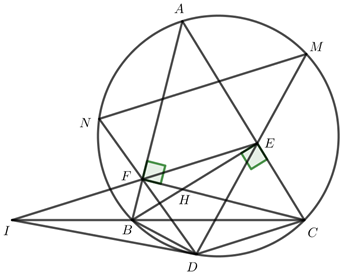
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Ta có ∠AEH=∠AFH=90o⇒∠AEH=∠AFH=90o⇒ E, F thuộc đường tròn đường kính AH
⇒⇒ A, E, H, F cùng thuộc một đường tròn
⇒AEHF⇒AEHF là tứ giác nội tiếp (dhnb).
Ta có ∠BEC=∠BFC=90o⇒∠BEC=∠BFC=90o⇒ BCEF là tứ giác nội tiếp (dhnb)
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O)(O)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID2=IB.ICID2=IB.IC.
Xét ΔIBDΔIBD và ΔIDCΔIDC có:
∠I∠I chung
∠IDB=∠ICD∠IDB=∠ICD (ID là tiếp tuyến của (O)(O))
⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).
c) DE, DF cắt đường tròn (O)(O) tại M và N. Chứng minh NM // EF.
Xét ΔIBEΔIBE và ΔIFCΔIFC có:
∠I∠I chung
∠IEB=∠ICF∠IEB=∠ICF (BCEF là tứ giác nội tiếp)
⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF (kết hợp b)
⇒ID2=IE.IF⇒IDIE=IFID⇒ID2=IE.IF⇒IDIE=IFID
Xét ΔIDFΔIDF và ΔIEDΔIED có:
∠I∠I chung
IDIE=IFID(cmt)IDIE=IFID(cmt)
⇒ΔIDF∼ΔIED⇒∠IDF=∠IED⇒ΔIDF∼ΔIED⇒∠IDF=∠IED (2 góc tương ứng)
Mặt khác ∠IDF=∠NMD∠IDF=∠NMD (ID là tiếp tuyến của (O)(O)) ⇒∠IED=∠NMD⇒∠IED=∠NMD (tc)
Mà hai góc này ở vị trí đồng vị ⇒⇒ NM // EF.

1: góc ABP=1/2*sđ cung AP=90 độ
=>BP//CH
góc ACP=1/2*sđ cung AP=90 độ
=>CP//BH
mà BP//CH
nên BHCP là hình bình hành
=>BC cắt HP tại trung điểm của mỗi đường
=>M là trung điểm của HP

A B C O E F H D I P Q K R M
a) Chứng minh AE.AC=AH.AD:
Xét \(\Delta\)AEH và \(\Delta\)ADC: ^AEH=^ADC(=900); ^DAC chung => \(\Delta\)AEH ~ \(\Delta\)ADC (g.g)
\(\Rightarrow\frac{AE}{AD}=\frac{AH}{AC}\Rightarrow AE.AC=AH.AD\)(đpcm).
b) Chứng minh P;H;Q thẳng hàng:
Ta nối 2 điểm P và Q với điểm H.
Xét đường tròn (I): Có AQ là tiếp tuyến; AEC là cát tuyến => ^AQE=^ACQ
Xét \(\Delta\)AEQ và \(\Delta\)AQC: ^QAC chung; ^AQE=^ACQ => \(\Delta\)AEQ ~ \(\Delta\)AQC (g.g)
\(\Rightarrow\frac{AQ}{AC}=\frac{AE}{AQ}\Rightarrow AQ^2=AE.AC\)
Lại có: \(AE.AC=AH.AD\Rightarrow AQ^2=AH.AD\Rightarrow\frac{AQ}{AH}=\frac{AD}{AQ}\)
Xét \(\Delta\)AHQ và \(\Delta\)AQD: ^DAQ chung; \(\frac{AQ}{AH}=\frac{AD}{AQ}\)=> \(\Delta\)AHQ ~ \(\Delta\)AQD (c.g.c)
\(\Rightarrow\)^AQH=^ADQ (1)
Ta thấy: AP và AQ là 2 tiếp tuyến của (I) => Tứ giác APIQ nội tiếp đường tròn (Tâm là trung điểm AI)
Dễ có tứ giác ADIQ nội tiếp đường tròn tâm là trung điểm AI (Do ^ADI=^AQI=900)
Từ đó suy ra: 5 điểm A;P;D;I;Q cùng thuộc 1 đường tròn => Tứ giác APDQ nội tiếp dường tròn
=> ^ADQ=^APQ (Cùng chắn cung AQ) (2)
Từ (1) và (2) => ^AQH=^APQ. Mà \(\Delta\)PAQ cân đỉnh A => ^APQ=^AQP => ^AQH=^AQP
Dễ thấy 2 tia QH và QP nằm cùng phía so với mặt phẳng bờ là AQ
=> P;H;Q là 2 điểm thẳng hàng (đpcm).
c) Chứng minh HP vuông với AK và KH vuông với AI:
Ở phần c) Mình sửa điểm P thành điểm R vì phần b) đã có điểm P rồi.
+) Ta có: Tứ giác BFEC nội tiếp (I) => ^ECB=^BFK hay ^KCE=^KFB
=> \(\Delta\)KBF ~ \(\Delta\)KEC (g.g) => \(\frac{KB}{KE}=\frac{KF}{KC}\Rightarrow KB.KC=KE.KF\)(3)
Xét đường tròn (O) có 2 cát tuyến KRA và KBC, ta có ngay tỉ số: \(\frac{KR}{KC}=\frac{KB}{KA}\Rightarrow KB.KC=KR.KA\)(4)
Từ (3) và (4) => \(KE.KF=KR.KA\)\(\Rightarrow\frac{KR}{KE}=\frac{KF}{KA}\)
=> \(\Delta\)KRF ~ \(\Delta\)KEA (c.g.c) => ^KRF=^KEA. Mà ^KRF+^FRA=1800
=> ^KEA+^FRA=1800 hay ^FRA+^FEA=1800 => Tứ giác ARFE nội tiếp đường tròn.
Mà tứ giác AFHE nội tiếp đường tròn => 5 điểm A;R;F;H;E cùng thuộc 1 đường tròn
=> Tứ giác ARFH nội tiếp đường tròn => ^ARH=^AFH.
Lại có: ^AFH=900 => ^ARH=900 => HR vuông góc AR hay HR vuông góc AK (ddpcm0.
+) Gọi giao điểm của tia RH và (O) là M => ^ARM=^ARH=900
Tứ giác ARBM nội tiếp đường trong nên ^ARM=^ABM (=900) => AB vuông góc BM
Lại thấy CF vuông góc AB => CF//BM hay CH//BM
Tứ giác ABMC nội tiếp đường tròn => ^ABM+^ACM=1800 => ^ACM=900
Tương tự ta c/m được: CM//BH
Xét tứ giác BHCM: CH//BM; CM//BH (cmt) => Tứ giác BHCM là hình bình hành
Do I là trung điểm BC nên H.I.M thẳng hàng => R;H;I thẳng hàng và IR vuông góc AK
Xét \(\Delta\)KAI: IR vuông AK; AD vuông KI; IR cắt AD tại H => H là trực tâm của \(\Delta\)KAI
=> KH vuông góc với AI (đpcm).
d) Chứng minh BC;EF;PQ đồng quy:
Vì EF cắt BC tại điểm K nên ta sẽ chứng minh K;P;Q là 3 điểm thẳng hàng.
Dễ có: Tứ giác APDI nội tiếp đường tròn => ^DPI=^DAI.
Mà ^DAI=^IKH (Cùng phụ góc AIK) => ^DPI=^IKH hay ^DPI=^DKP
Xét \(\Delta\)KPD: ^DKP + ^KDP+^KPD = 1800 => ^DPI + ^KDP + ^KPD = 1800
=> ^KPI + ^KDP = 1800 (5)
Để ý rằng tứ giác PDIQ nội tiếp đường tròn => ^IQP=^KDP.
Mà \(\Delta\)PIQ cân đỉnh I => ^IQP=^IPQ => ^KDP=^IPQ (6)
Từ (5) và (6) => ^KPI + ^IPQ = 1800 => ^KPQ = 1800 => 3 điểm K;P;Q thẳng hàng.
Qua đó, ta suy ra được BC;EF;PQ đồng quy (đpcm).

Không thấy câu a) của bạn đâu nên mình chứng minh câu b) luôn nhé.
Dễ thấy \(\widehat{BHD}=\widehat{BCA}\) vì cùng phụ với \(\widehat{HBC}\).
Lại có \(\widehat{BKD}=\widehat{BKA}=\widehat{BCA}\) nên suy ra \(\widehat{BHD}=\widehat{BKD}\) hay \(\widehat{BHK}=\widehat{BKI}\).
Mặt khác, tam giác AEH vuông tại E có trung tuyến EI nên \(EI=\dfrac{AH}{2}=IH\) \(\Rightarrow\Delta IEH\) cân tại I \(\Rightarrow\widehat{IHE}=\widehat{IEH}=\widehat{IEB}\)
Mà \(\widehat{IHE}=\widehat{BHK}=\widehat{BKI}\) \(\Rightarrow\widehat{IEB}=\widehat{IKB}\), từ đó suy ra tứ giác IEKB nội tiếp. (đpcm)