Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không thấy câu a) của bạn đâu nên mình chứng minh câu b) luôn nhé.
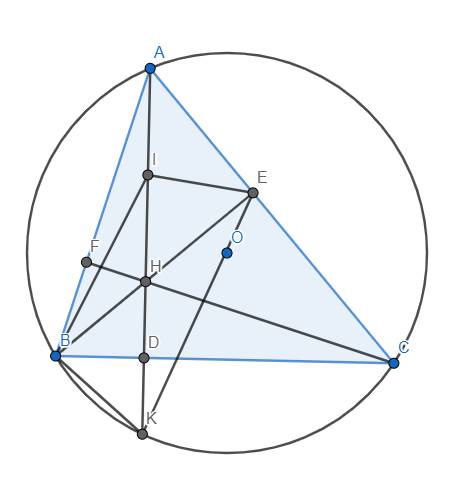
Dễ thấy \(\widehat{BHD}=\widehat{BCA}\) vì cùng phụ với \(\widehat{HBC}\).
Lại có \(\widehat{BKD}=\widehat{BKA}=\widehat{BCA}\) nên suy ra \(\widehat{BHD}=\widehat{BKD}\) hay \(\widehat{BHK}=\widehat{BKI}\).
Mặt khác, tam giác AEH vuông tại E có trung tuyến EI nên \(EI=\dfrac{AH}{2}=IH\) \(\Rightarrow\Delta IEH\) cân tại I \(\Rightarrow\widehat{IHE}=\widehat{IEH}=\widehat{IEB}\)
Mà \(\widehat{IHE}=\widehat{BHK}=\widehat{BKI}\) \(\Rightarrow\widehat{IEB}=\widehat{IKB}\), từ đó suy ra tứ giác IEKB nội tiếp. (đpcm)

câu a) bạn sử dụng tính chất của 3 đường cao là được.
b) bạn chứng minh là tam giác ABK là tam giác vuông do chắn nửa đường tròn
sau đó xét hai tam giác vuông ACD và AKB sao cho đồng dạng : có \(\widehat{ACD}=\widehat{AKB}\)do cùng chắn cung AB
sau đó bạn suy ra tỷ số đồng dạng rồi nhân chéo là xong.
c)
bạn xét hai tam giác MAB vad MCK sao cho đồng dạng do
hai góc M bằng nhau do đối đỉnh
góc MKC= góc MBA cùng chắn cung AC
rồi suy ra 2 tam giác đó dồng dạng rồi suy ra tỉ số đồng dạng rồi nhân chéo
d câu này ta có \(\hept{\begin{cases}CF\perp AB\\KB\perp AB\end{cases}\Rightarrow CF//KB\Leftrightarrow CH//KB}\)
\(\hept{\begin{cases}BE\perp AC\\KC\perp AC\end{cases}\Rightarrow BE//CK\Leftrightarrow BH//CK}\)
TỪ 2 ĐIỀU TRÊN ta suy ra được tứ giác CHBK LÀ HÌNH BÌNH HÀNH
TỪ ĐIỀU ĐÓ SUY RA I là giao diểm của hai đường chéo suy ra i là trung điểm của HK suy ra H,I,K thằng hàng

A B C O E F H D I P Q K R M
a) Chứng minh AE.AC=AH.AD:
Xét \(\Delta\)AEH và \(\Delta\)ADC: ^AEH=^ADC(=900); ^DAC chung => \(\Delta\)AEH ~ \(\Delta\)ADC (g.g)
\(\Rightarrow\frac{AE}{AD}=\frac{AH}{AC}\Rightarrow AE.AC=AH.AD\)(đpcm).
b) Chứng minh P;H;Q thẳng hàng:
Ta nối 2 điểm P và Q với điểm H.
Xét đường tròn (I): Có AQ là tiếp tuyến; AEC là cát tuyến => ^AQE=^ACQ
Xét \(\Delta\)AEQ và \(\Delta\)AQC: ^QAC chung; ^AQE=^ACQ => \(\Delta\)AEQ ~ \(\Delta\)AQC (g.g)
\(\Rightarrow\frac{AQ}{AC}=\frac{AE}{AQ}\Rightarrow AQ^2=AE.AC\)
Lại có: \(AE.AC=AH.AD\Rightarrow AQ^2=AH.AD\Rightarrow\frac{AQ}{AH}=\frac{AD}{AQ}\)
Xét \(\Delta\)AHQ và \(\Delta\)AQD: ^DAQ chung; \(\frac{AQ}{AH}=\frac{AD}{AQ}\)=> \(\Delta\)AHQ ~ \(\Delta\)AQD (c.g.c)
\(\Rightarrow\)^AQH=^ADQ (1)
Ta thấy: AP và AQ là 2 tiếp tuyến của (I) => Tứ giác APIQ nội tiếp đường tròn (Tâm là trung điểm AI)
Dễ có tứ giác ADIQ nội tiếp đường tròn tâm là trung điểm AI (Do ^ADI=^AQI=900)
Từ đó suy ra: 5 điểm A;P;D;I;Q cùng thuộc 1 đường tròn => Tứ giác APDQ nội tiếp dường tròn
=> ^ADQ=^APQ (Cùng chắn cung AQ) (2)
Từ (1) và (2) => ^AQH=^APQ. Mà \(\Delta\)PAQ cân đỉnh A => ^APQ=^AQP => ^AQH=^AQP
Dễ thấy 2 tia QH và QP nằm cùng phía so với mặt phẳng bờ là AQ
=> P;H;Q là 2 điểm thẳng hàng (đpcm).
c) Chứng minh HP vuông với AK và KH vuông với AI:
Ở phần c) Mình sửa điểm P thành điểm R vì phần b) đã có điểm P rồi.
+) Ta có: Tứ giác BFEC nội tiếp (I) => ^ECB=^BFK hay ^KCE=^KFB
=> \(\Delta\)KBF ~ \(\Delta\)KEC (g.g) => \(\frac{KB}{KE}=\frac{KF}{KC}\Rightarrow KB.KC=KE.KF\)(3)
Xét đường tròn (O) có 2 cát tuyến KRA và KBC, ta có ngay tỉ số: \(\frac{KR}{KC}=\frac{KB}{KA}\Rightarrow KB.KC=KR.KA\)(4)
Từ (3) và (4) => \(KE.KF=KR.KA\)\(\Rightarrow\frac{KR}{KE}=\frac{KF}{KA}\)
=> \(\Delta\)KRF ~ \(\Delta\)KEA (c.g.c) => ^KRF=^KEA. Mà ^KRF+^FRA=1800
=> ^KEA+^FRA=1800 hay ^FRA+^FEA=1800 => Tứ giác ARFE nội tiếp đường tròn.
Mà tứ giác AFHE nội tiếp đường tròn => 5 điểm A;R;F;H;E cùng thuộc 1 đường tròn
=> Tứ giác ARFH nội tiếp đường tròn => ^ARH=^AFH.
Lại có: ^AFH=900 => ^ARH=900 => HR vuông góc AR hay HR vuông góc AK (ddpcm0.
+) Gọi giao điểm của tia RH và (O) là M => ^ARM=^ARH=900
Tứ giác ARBM nội tiếp đường trong nên ^ARM=^ABM (=900) => AB vuông góc BM
Lại thấy CF vuông góc AB => CF//BM hay CH//BM
Tứ giác ABMC nội tiếp đường tròn => ^ABM+^ACM=1800 => ^ACM=900
Tương tự ta c/m được: CM//BH
Xét tứ giác BHCM: CH//BM; CM//BH (cmt) => Tứ giác BHCM là hình bình hành
Do I là trung điểm BC nên H.I.M thẳng hàng => R;H;I thẳng hàng và IR vuông góc AK
Xét \(\Delta\)KAI: IR vuông AK; AD vuông KI; IR cắt AD tại H => H là trực tâm của \(\Delta\)KAI
=> KH vuông góc với AI (đpcm).
d) Chứng minh BC;EF;PQ đồng quy:
Vì EF cắt BC tại điểm K nên ta sẽ chứng minh K;P;Q là 3 điểm thẳng hàng.
Dễ có: Tứ giác APDI nội tiếp đường tròn => ^DPI=^DAI.
Mà ^DAI=^IKH (Cùng phụ góc AIK) => ^DPI=^IKH hay ^DPI=^DKP
Xét \(\Delta\)KPD: ^DKP + ^KDP+^KPD = 1800 => ^DPI + ^KDP + ^KPD = 1800
=> ^KPI + ^KDP = 1800 (5)
Để ý rằng tứ giác PDIQ nội tiếp đường tròn => ^IQP=^KDP.
Mà \(\Delta\)PIQ cân đỉnh I => ^IQP=^IPQ => ^KDP=^IPQ (6)
Từ (5) và (6) => ^KPI + ^IPQ = 1800 => ^KPQ = 1800 => 3 điểm K;P;Q thẳng hàng.
Qua đó, ta suy ra được BC;EF;PQ đồng quy (đpcm).

tứ giác BFEC có hai góc kề nhau cùng nhìn đoạn BC dưới một góc vuông : BFCˆ=BECˆ(=90)BFC^=BEC^(=90) ==> Tức giác BFEC là tứ giác nội tiếp
==> 4 điểm B,E,F,C cùng thuộc một đường tròn.

Giải chi tiết:
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Ta có ∠AEH=∠AFH=90o⇒∠AEH=∠AFH=90o⇒ E, F thuộc đường tròn đường kính AH
⇒⇒ A, E, H, F cùng thuộc một đường tròn
⇒AEHF⇒AEHF là tứ giác nội tiếp (dhnb).
Ta có ∠BEC=∠BFC=90o⇒∠BEC=∠BFC=90o⇒ BCEF là tứ giác nội tiếp (dhnb)
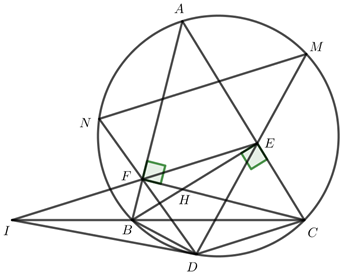
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O)(O)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID2=IB.ICID2=IB.IC.
Xét ΔIBDΔIBD và ΔIDCΔIDC có:
∠I∠I chung
∠IDB=∠ICD∠IDB=∠ICD (ID là tiếp tuyến của (O)(O))
⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).
c) DE, DF cắt đường tròn (O)(O) tại M và N. Chứng minh NM // EF.
Xét ΔIBEΔIBE và ΔIFCΔIFC có:
∠I∠I chung
∠IEB=∠ICF∠IEB=∠ICF (BCEF là tứ giác nội tiếp)
⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF (kết hợp b)
⇒ID2=IE.IF⇒IDIE=IFID⇒ID2=IE.IF⇒IDIE=IFID
Xét ΔIDFΔIDF và ΔIEDΔIED có:
∠I∠I chung
IDIE=IFID(cmt)IDIE=IFID(cmt)
⇒ΔIDF∼ΔIED⇒∠IDF=∠IED⇒ΔIDF∼ΔIED⇒∠IDF=∠IED (2 góc tương ứng)
Mặt khác ∠IDF=∠NMD∠IDF=∠NMD (ID là tiếp tuyến của (O)(O)) ⇒∠IED=∠NMD⇒∠IED=∠NMD (tc)
Mà hai góc này ở vị trí đồng vị ⇒⇒ NM // EF.

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)