Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì BCNN(15,20,5)=60 nên cứ 60p hay cứ 1 tiếng thì cả 3 xe rời cùng 1 lúc
Do đó lúc 5+1=6(giờ) thì lại có 3 xe rời bến cùng 1 lúc

Gọi khoảng thời gian để taxi và xe buýt cùng rời bến giữa 2 lần liên tiếp là : a (phút)
Sau a phút thì có xe taxi rời bến thì a chia hết cho 12
Sau a phút thì có xe buýt rời bến nên a chia hết cho 15
=> a chia hết cho 12 và 15
Mà thời gian ta tính nhỏ nhất nên a nhỏ nhất => a nhỏ nhất => a là BCNN của 12 và 15
Ta có:
10 = 2 . 5
12 = 2^2 . 3
=> BCNN(10;12) = 2^2.3.5 = 60
=> sau 60 phút thì một xe buýt và một taxi cùng rời bến.
Đổi 60 phút = 1 giờ
Ta có : 6 + 1 = 7
Vậy : Lúc 7 giờ lại có một xe buýt và một tắc xi cùng rời Bến
chúc bạn học tốt
Gọi khoảng thời gian để taxi và xe buýt cùng rời bến giữa 2 lần liên tiếp gọi là t(phút)
Sau t phút thì có xe taxi rời bến nên t chia hết cho 12
Sau t phút thì có xe buýt rời bến nên t chia hết cho 15
=> t chia hết cho 12 và 15
mà t nhỏ nhất nên t là BCNN(12,15)
Ta có: 12=2^2.3
15=3.5
=> t=BCNN(12,15)= 2^2.3.5=60
Vậy lúc 7h lại có 1 taxi và 1 xe buýt rời bến cùng lúc lần tiếp theo

Gọi t/g từ lúc xe taxi và xe buýt cùng trời bến lần này đến lúc xe taxi và xe buýt cùng rời bến lần tiếp theo là a ( phút )
Ta có \(a⋮10;a⋮12\) và a là BCNN(10,12) ( vì a nhỏ nhất )
Từ đây ta tìm đc a là 60
Vậy lúc 7h lại có 1 xe taxi và 1 xe buýt cùng rời bến
Gọi x (phút) (x ∈ N) là thời gian từ lúc taxi và xe buýt cùng rời bến lần này đến lúc taxi và xe buýt cùng rời bến lần tiếp theo.
Ta có: x ⋮ 10 và x ⋮ 12
Vì m nhỏ nhất nên m là BCNN(10; 12)
Ta có: 10= 2.5
12=22.3
BCNN(10;12)=22.3.5=60
Vậy sau 60 phút = 1 giờ thì taxi và xe buýt cùng rời bến lần tiếp theo. Lúc đó là 6 + 1 = 7 giờ.
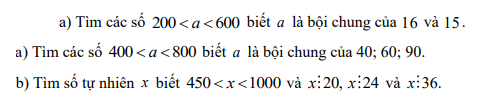
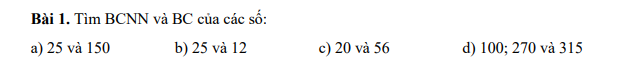
Bài 3:
a: \(a\in\left\{240;480\right\}\)
b: b=720