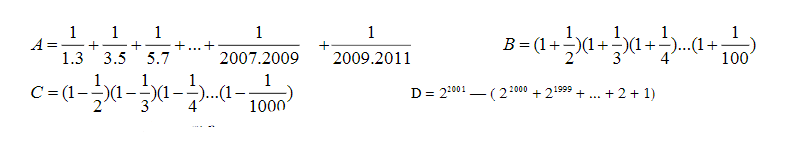VN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QN
2
VT
10 tháng 9 2016
(0,25)^4 . 1024 = (0,25)^4 . 2^10 = (0,25)^4 . 2^4 . 2^6 = (0,25 . 2)^4 . 2^6 = (0,5)^4 . 2^4. 2^2 = (0,5 . 2)^4 . 2^2 = 1^4 . 2^2 = 1 . 4 = 4
PA
0
LM
8 tháng 1 2016
S=1.2+2.3+3.4+.............+n(n+1)
=1(1+1) + 2(2+1) + 3(3+1) +...+n(n+1)
=(1^2 + 2^2 + 3^2 +...+ n^2) + (1 + 2 + 3 + ...+ n)
Ta có các công thức:
1^2 + 2^2 + 3^2 +...+ n^2 = n(n+1)(2n+1)/6
1 + 2 + 3 + ...+ n = n(n+1)/2
Thay vào ta có:
S = n(n+1)(2n+1)/6 + n(n+1)/2
=n(n+1)/2[(2n+1)/3 + 1]
=n(n+1)(n+2)/3
AM
6 tháng 5 2017
Bài 1 :
\(A=1\cdot2+2\cdot3+3\cdot4+...+n\cdot\left(n+1\right)\)
\(\Rightarrow3A=1\cdot2\cdot3+2\cdot3\cdot3+3\cdot4\cdot3+...+n\cdot\left(n+1\right)\cdot3\)
\(=1\cdot2\cdot3+2\cdot3\cdot\left(4-1\right)+...+n\cdot\left(n+1\right)\cdot\left[\left(n+2\right)-\left(n-1\right)\right]\)
\(=1\cdot2\cdot3+2\cdot3\cdot4-1\cdot2\cdot3+2\cdot3\cdot4-3\cdot4\cdot5+...+n\left(n+1\right)\left(n+2\right)-\left(n-1\right)n\left(n+1\right)\)
\(=n\left(n+1\right)\left(n+2\right)\)
\(\Rightarrow A=\frac{n\left(n+1\right)\left(n+2\right)}{3}\)
6 tháng 5 2017
Bài 1.
A = 1.2 + 2.3 + 3.4 + ... + n.(n + 1)
3A = 1.2.3 + 2.3.3 + 3.4.3 + ... + n.(n + 1).3
3A = 1.2.3 + 2.3.(4 - 1) + 3.4.(5 - 2) + ... + n.(n + 1).(n + 2 - n - 1)
3A = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ... + n.(n + 1).(n + 2 ) - (n - 1).n.(n + 1)
3A = n.(n + 1).(n + 2)
A = n.(n + 1).(n + 2) : 3
Bài 2.
B = 1.2.3 + 2.3.4 + ... + (n - 1).n.(n + 1)
4B = 1.2.3.4 + 2.3.4.4 + ... + (n - 1).n.(n + 1).4
4B = 1.2.3.4 + 2.3.4.(5 - 1) + .... + (n - 1).n.(n + 1).(n + 2 - n - 2)
4B = 1.2.3.4 + 2.3.4.5 - 1.2.3.4 + ... + (n - 1).n.(n + 1).(n + 2) - (n - 2).(n - 1).n.(n + 1)
4B = (n - 1).n.(n + 1).(n + 2)
B = (n - 1).n.(n + 1).(n + 2) : 4
Xong rồi nhé anh !
14 tháng 7 2016
Bài 1:
Ta có:
\(y-x=25\Rightarrow y=25+x\)
Mà \(7x=4y\Rightarrow7x=4\cdot\left(25+x\right)\)
\(7x=100+4x\)
\(\Rightarrow7x-4x=100\)
\(3x=100\)
\(x=\frac{100}{3}\)
2 tháng 11 2023
bài 1 :
Ta có: 7x=4y ⇔ x/4=y/7
áp dụng tính chất dãy tỉ số bằng nhau ta có
x/4=y/7=(y-x)/(7-4)=100/3
⇒x= 4 x 100/3=400/3 ; y = 7 x 100/3=700/3
bài 2
ta có x/5 = y/6 ⇔ x/20=y/24
y/8 = z/7 ⇔ y/24=z/21
⇒x/20=y/24=z/21
ADTCDTSBN(bài 1 có)
x/20=y/24=z/21=(x+y)/(20+24)=69/48=23/16
⇒x= 20 x 23/16 = 115/4
y= 24x 23/16=138/2
z=21x23/16=483/16
30 tháng 8 2021
a: Ta có: \(A=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{2009\cdot2011}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2009\cdot2011}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2010}{2011}=\dfrac{1005}{2011}\)
b: Ta có: \(B=\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)+...+\left(1+\dfrac{1}{100}\right)\)
\(=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{101}{100}\)
\(=\dfrac{101}{2}\)
HP
30 tháng 8 2021
\(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2007.2009}+\dfrac{1}{2009.2011}\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2007}-\dfrac{1}{2009}+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{2011}\right)\)
\(=\dfrac{1005}{2011}\)
HC
0
9 tháng 7 2017
các bạn trả lời bài 1 cũng được trả lời xong thì báo cho mình để mình k nha
HT
6 tháng 12 2017
bai 1
a,17.64+68.34=34.32+68.34=34.(68+32)=34.100=3400
b,37.63+64.163=37.63+63.163+163=63(37+60)+163=63.100+163=6300+163=6463
c,163.68+16.272=136.68+32.136=136(68+32)=136.100=13600
d,26.13+74.14=26.13+74.13+74=13.(74+26)+74=13.100+74=1300+74=1374