Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho mạch điện như hình vẽ: R1=6 ôm, R2=12 ôm, R3=4 ôm, I1=1A. Tính U1,U2,U3,Uab=?
a. \(R=R1+\left(\dfrac{R2.R3}{R2+R3}\right)=2+\left(\dfrac{6.3}{6+3}\right)=4\left(\Omega\right)\)
b. \(I=I1=I23=\dfrac{U}{R}=\dfrac{12}{4}=3A\left(R1ntR23\right)\)
\(U23=U2=U3=I13.R23=3\left(\dfrac{6.3}{6+3}\right)=6\left(V\right)\)(R2//R3)
\(\left\{{}\begin{matrix}I2=U2:R2=6:6=1A\\I3=U3:R3=6:3=2A\end{matrix}\right.\)
c. \(U_d=U_{23}=6V\Rightarrow\) đèn sáng bình thường.
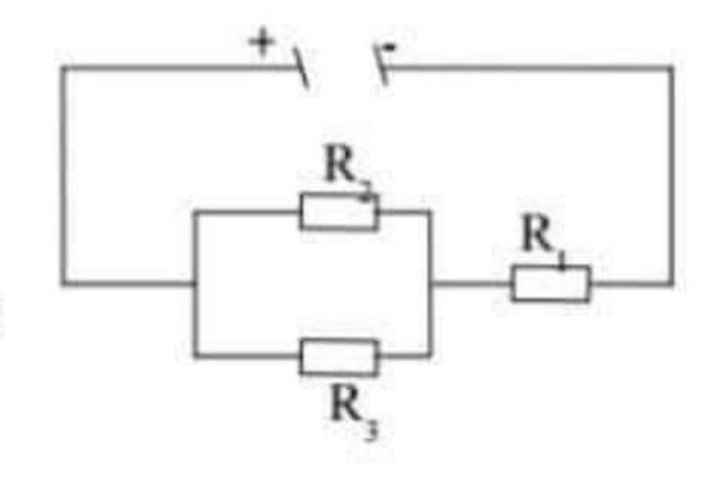
a, \(=>R5nt\left[\left(R1//R3\right)nt\left(R2//R4\right)\right]\)
\(=>Rtd=R5+\dfrac{R1R3}{R1+R3}+\dfrac{R2.R4}{R2+R4}=1,2+\dfrac{8.12}{8+12}+\dfrac{8.24}{8+24}\)\(=12\left(om\right)\)
b,\(=>Im=\dfrac{4}{12}=\dfrac{1}{3}A=I5=I13=I24\)
\(=>U13=\dfrac{1}{3}\left(\dfrac{8.12}{8+12}\right)=1,6V=U1=U3\)
\(=>I1=\dfrac{1,6}{8}=0,2A,I3=\dfrac{1,6}{12}=\dfrac{2}{15}A\)
\(=>U24=\dfrac{1}{3}\left(\dfrac{8,24}{8+24}\right)=2V=U2=U4\)
\(=>I2=\dfrac{2}{8}=0,25A,I4=\dfrac{2}{24}=\dfrac{1}{12}A\)
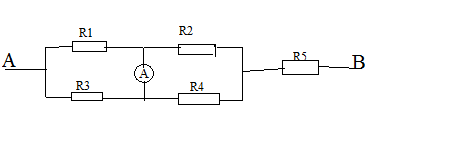
c, giả sử chiều dòng điện qua ampe kế từ M đến N
\(=>I1=Ia+I2=>Ia=I1-I2=0,2-0,25=-0,05A\)
=>chiều dòng điện phải từ N tới M =>số chỉ ampe kế là 0,05A
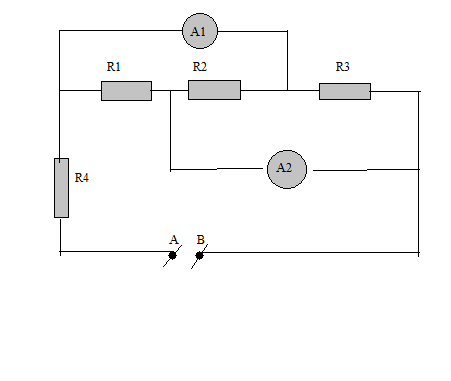
ta thấy \(\dfrac{R_1}{R_2}=\dfrac{R_3}{R_4}=2\) => mạch cầu cân bằng => I5=0 U5=0
khi K đóng \(R_{1234}=\dfrac{\left(R_1+R_3\right)\left(R_2+R_4\right)}{R_1+R_2+R_3+R_4}=4\left(\Omega\right)\)
\(R_{td}=\dfrac{R_6.R_{1234}}{R_6+R_{1234}}\)
\(\Rightarrow I_A=I=\dfrac{U_{AB}}{R_{td}}=\dfrac{48}{2}=24\left(A\right)\)
em đang ôn hsg lí 9 à :???
Dạng mạch điện [ R1 nt (R2 // R3) ] // R4
a) Điện trở của đoạn mạch ACD là:
\(R_{ACD}=R_1+\dfrac{R_2.R_3}{R_2+R_3}=15+\dfrac{20.20}{20+20}=25\left(\Omega\right)\)
Điện trở tương đương của toàn mạch điện là:
\(R_{tđ}=\dfrac{R_{ACD}.R_4}{R_{ACD}+R_4}=\dfrac{25.10}{25+10}=\dfrac{50}{7}\left(\Omega\right)\)
Vậy.....
b) Vì ampe kế nối tiếp với đèn Đ4 ⇒ \(I_4=I_A=5\left(A\right)\)
Vì R4 // RACB ⇒ UAB = U4 = I4.R4 = 5.10 = 50 (V)
Vì R1 nt RCB ⇒ \(I_1=I_{ACB}=\dfrac{U_{AB}}{R_{ACB}}=\dfrac{50}{25}=2\left(A\right)\)
\(U_{AC}=U_1=I_1.R_1=2.15=30\left(V\right)\)
Vậy....
Trong đó R1=2 ôm, R2=6 ôm, R3=4 ôm, R4=10 ôm. Hiệu điện thế Uab=28v
Tóm tắt:
\(R_1=2\Omega\\ R_2=6\Omega\\ R_3=4\Omega\\ R_4=10\Omega\\ U_{AB}=28V\\ a,R_{tđ}=?\\ b,I_1?\\ I_2=?\\ I_3=?\\ I_4=?\\ c,U_1=?\\ U_2=?\)
Giải:
Cấu tạo: R1nt[R4//(R2ntR3)]
\(R_{23}=R_2+R_3=6+4=10\left(\Omega\right)\)
\(R_{234}=\dfrac{R_4\cdot R_{23}}{R_4+R_{23}}=5\Omega\)
\(R_{tđ}=R_1+R_{234}=7\Omega\)
b,\(I_1=I=\dfrac{U_{AB}}{R_{tđ}}=\dfrac{28}{7}=4\left(A\right)\)
\(I_{234}=I_1=4\left(A\right)\)
\(\Rightarrow U_{23}=U_4=U_{234}=I_{234}\cdot R_{234}=4\cdot5=20\left(V\right)\)
\(I_4=\dfrac{U_4}{R_4}=\dfrac{20}{10}=2\left(A\right)\)
\(I_2=I_3=I_{23}=\dfrac{U_{23}}{R_{23}}=\dfrac{20}{10}=2\left(A\right)\)
c,\(U_1=R_1\cdot I_1=2\cdot4=8\left(V\right)\)
\(U_2=I_2\cdot R_2=2\cdot6=12\left(V\right)\)
a)CTM: \(R_1nt\left(\left(R_2ntR_3\right)//R_4\right)\)
\(R_{23}=R_2+R_3=7+5=12\Omega\)
\(R_{234}=\dfrac{R_{23}\cdot R_4}{R_{23}+R_4}=\dfrac{12\cdot11}{12+11}=\dfrac{132}{23}\Omega\)
\(R_{tđ}=R_1+R_{234}=3+\dfrac{132}{23}=\dfrac{201}{23}\Omega\)
b)\(I_1=I_{234}=I_{AB}=\dfrac{U_{AB}}{R_{AB}}=\dfrac{30}{\dfrac{201}{23}}=\dfrac{230}{67}A\approx3,4A\)
\(U_{23}=U_4=U-U_1=30-I_1\cdot R_1=30-\dfrac{230}{67}\cdot3=\dfrac{1320}{67}V\)
\(I_4=\dfrac{U_4}{R_4}=\dfrac{\dfrac{1320}{67}}{11}=\dfrac{120}{67}A\approx1,79A\)
\(I_2=I_3=I_{23}=\dfrac{U_{23}}{R_{23}}=\dfrac{\dfrac{1320}{67}}{12}=\dfrac{110}{67}A\approx1,64A\)