Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

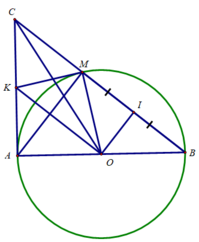
a) Tam giác AMB nội tiếp đường tròn (O) có AB là đường kính
⇒ ΔAMB vuông tại M hay ∠(AMB) = 90o
⇒ AM là đường cao của tam giác ABC
Xét tam giác ABC vuông tại A có AM là đường cao
⇒ A C 2 = CM.CB (hệ thức liên hệ giữa cạnh và đường cao)

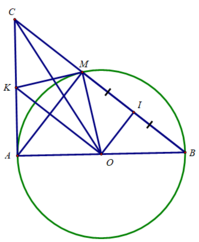
c) Tam giác CMA vuông tại M có MK là trung tuyến
⇒ MK = KA = KC
Xét Δ KAO và Δ KMO có:
KA = KM
KO là cạnh chung
AO = MO ( = bán kính (O))
⇒ Δ KAO = Δ KMO (c.c.c)
⇒ ∠(KAO) = ∠(KMO)
Mà ∠(KAO) = 90 0 ⇒ ∠(KMO) = 90 0
⇒ KM là tiếp tuyến của (O)

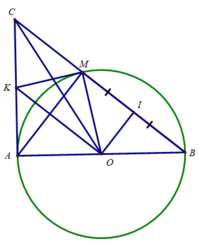
b) Tam giác ACO vuông tại A ⇒ Tâm đường tròn ngoại tiếp tam giác ACO là trung điểm của CO (1)
Xét tam giác AMB có:
I là trung điểm của AM
O là trung điểm của AB
⇒ IO là đường trung bình của tam giác AMB
⇒ IO // AM
Mà AM ⊥ MB ⇒ IO ⊥ MB
Tam giác CIO vuông tại I ⇒ Tâm đường tròn ngoại tiếp tam giác CIO là trung điểm của CO (2)
Từ (1) và (2) ⇒ 4 điểm A, I, C, O cùng thuộc một đường tròn

Bài 1:
a,
OM là đường trung bình của tam giác BAC => OM = 1/2*BC
OM = 1/2*AB
=> AB=BC (đpcm).
b,
Tam giác ABC đều => BC = 2*r(O)
MN là đường trung bình của tam giác ABC => MN = 1/2*AB = r(O) = OM = OB =BN => BOMN là hình thoi.

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>AM\(\perp\)CB tại M
=>AM là đường cao của ΔCAB
Xét ΔBAC vuông tại A có AM là đường cao
nên \(AC^2=CM\cdot CB\)
b: ΔOMB cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)MB tại I
Xét tứ giác CAOI có \(\widehat{CAO}+\widehat{CIO}=90^0+90^0=180^0\)
nên CAOI là tứ giác nội tiếp
=>C,A,O,I cùng thuộc một đường tròn
c: ΔCMA vuông tại M
mà MK là đường trung tuyến
nên KA=KM
Xét ΔKAO và ΔKMO có
KA=KM
OA=OM
KO chung
Do đó: ΔKAO=ΔKMO
=>\(\widehat{KAO}=\widehat{KMO}\)
=>\(\widehat{KMO}=90^0\)
=>KM là tiếp tuyến của (O)