Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\frac{24}{146}=\frac{24.13}{146.13}=\frac{312}{1898}\)
\(\frac{6}{13}=\frac{6.146}{13.146}=\frac{876}{1898}\)
b) \(\frac{7}{30}=\frac{7.60.40}{30.60.40}=\frac{16800}{72000}\)
\(\frac{13}{60}=\frac{13.30.40}{60.30.40}=\frac{15600}{72000}\)
\(\frac{-9}{40}=\frac{-9.30.60}{40.30.60}=\frac{-16200}{72000}\)
c)\(\frac{17}{60}=\frac{17.18.90}{60.18.90}=\frac{27540}{97200}\)
\(\frac{-5}{18}=\frac{5.60.90}{18.60.90}=\frac{27000}{97200}\)
\(\frac{-64}{90}=\frac{-64.18.60}{90.18.60}=\frac{-69120}{97200}\)
Mệt quá đi

a) MSC : 60
17/20= 17.3/20.3= 51/60
13/15= 13.4/15.4=52/60
41/60=41.1/60.1=41/60
Lúc chiều mk vừa làm xong nên ko sai đâu. Thầy chữa bài này luôn rồi
A)51/60;52/60;41/60
B)748/2244;1122/2244;2057/2244
C)300/2400;2280/2400;1280/2400
Tự rút gọn nhé...
Câu d thì mình...

bài 1 a)
\(\frac{15}{7}\times\frac43+\frac63\)
=\(\frac{60}{21}+\frac63\)
=\(\frac{60}{21}+\frac{42}{21}\)
=\(\frac{102}{21}\)
=\(\frac{34}{7}\)
b)\(\frac{-13}{41}\times\frac{17}{11}\times\frac{11}{17}\)
=\(\frac{-13}{41}\times\left(\frac{17}{11}\times\frac{11}{17}\right)\)
=\(\frac{-13}{41}\times1\)
=\(\frac{-13}{41}\)

cái thứ nhất mẫu số chung là 1898
cái thứ hai mẫu số chung là 360

1/ ĐÁP ÁN:
\(\frac{-9}{33}=\frac{3}{-11}\); \(\frac{15}{9}=\frac{5}{3}\); \(\frac{-12}{19}=\frac{60}{-95}\)
2/ ĐÁP ÁN:
\(\frac{-7}{20}=\frac{3}{-18}=\frac{-9}{54}\ne\frac{12}{18}=\frac{-10}{-15}\ne\frac{14}{20}\)
3/ ĐÁP ÁN:
\(\frac{2}{3}=\frac{40}{60}\); \(\frac{3}{4}=\frac{45}{60}\); \(\frac{4}{5}=\frac{48}{60}\); \(\frac{5}{6}=\frac{50}{60}\)

bạn ơi có thể g cho mình ko quy dong hay so sánh phan so 9/10 va 10/11

a)\(\left(4\frac{5}{37}-3\frac45+8\frac{15}{29}\right)-\left(3\frac{5}{57}-6\frac{14}{29}\right)\)
=\(4\frac{5}{37}-3\frac45+8\frac{15}{29}-3\frac{5}{37}+6\frac{14}{29}\)
=\(\left(4\frac{5}{37}-3\frac{5}{37}\right)+\left(8\frac{15}{29}+6\frac{14}{29}\right)-3\frac45\)
=\(\left\lbrack\left(4-3\right)+\left(\frac{5}{37}-\frac{5}{37}\right)\right\rbrack+\left\lbrack\left(8+6\right)+\left(\frac{15}{29}\right.\right.\)+\(\frac{14}{29})\) -\(\frac{19}{5}\)
=\(1+0+14+1-\frac{19}{5}\)
=\(15+1-\frac{19}{5}\)
=\(16-\frac{19}{5}\)
=\(\frac{80}{5}-\frac{19}{5}\)
=\(\frac{61}{5}\)
29. Quy đồng mẫu các phân số sau:
a) và
và  ; b)
; b)  và
và  ; c)
; c) 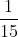 và -6.
và -6.
Giải.
a)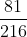 và
và 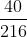 ; b)
; b) 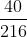 và
và 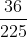 ; c)
; c) 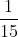 và
và 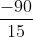
30. Quy đồng mẫu các phân số sau:
a) và
và  ; b)
; b)  và
và  ;
;
c) ; d)
; d) 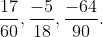
Giải.
a) và
và  ; b)
; b)  và
và  (chú ý rằng
(chú ý rằng  =
=  )
)
c) ; d)
; d)  .
.
31. Hai phân số sau đây có bằng nhau không?
a) và
và  ; b)
; b)  và
và  .
.
Hướng dẫn : Rút gọn để được những phân số tối giản rồi so sánh: