
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
Ta có: \(\sqrt{4x^2-12x+9}=4\)
\(\Leftrightarrow\left|2x-3\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=4\\2x-3=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=7\\2x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Bài 2:
a: Ta có: \(\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}\)
\(=\sqrt{17-12\sqrt{2}}+\sqrt{17+12\sqrt{2}}\)
\(=3-2\sqrt{2}+3+2\sqrt{2}\)
=6
b: Ta có: \(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\)
\(=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\)
\(=2\sqrt{2}\)

\(\sqrt{9x+9}-2\sqrt{\dfrac{x+1}{4}}=4\left(đk:x\ge-1\right)\)
\(\Leftrightarrow3\sqrt{x+1}-\sqrt{x+1}=4\)
\(\Leftrightarrow2\sqrt{x+1}=4\)
\(\Leftrightarrow\sqrt{x+1}=2\Leftrightarrow x+1=4\Leftrightarrow x=3\left(tm\right)\)

Bài 2:
e) \(\sqrt{4x-8}-12\sqrt{\dfrac{x-2}{9}}=\sqrt{x-2}-12\left(đk:x\ge2\right)\)
\(\Leftrightarrow\sqrt{4}.\sqrt{x-2}-12.\sqrt{\dfrac{1}{9}}.\sqrt{x-2}=\sqrt{x-2}-12\)
\(\Leftrightarrow2\sqrt{x-2}-4\sqrt{x-2}=\sqrt{x-2}-12\)
\(\Leftrightarrow3\sqrt{x-2}=12\)
\(\Leftrightarrow\sqrt{x-2}=4\)
\(\Leftrightarrow x-2=16\Leftrightarrow x=18\left(tm\right)\)

c: Ta có: \(\sqrt{x+4\sqrt{x-4}}=5\)
\(\Leftrightarrow\sqrt{x-4}+2=5\)
\(\Leftrightarrow\sqrt{x-4}=3\)
\(\Leftrightarrow x-4=9\)
hay x=13
c: Ta có: √x+4√x−4=5x+4x−4=5
⇔√x−4+2=5⇔x−4+2=5
⇔√x−4=3⇔x−4=3
⇔x−4=9⇔x−4=9
hay x=13

Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)

Bài 8:
\(1,P=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\\ 2,P=2\Leftrightarrow2\sqrt{x}+4=3\sqrt{x}\Leftrightarrow\sqrt{x}=4\\ \Leftrightarrow x=16\left(tm\right)\)
Bài 9:
\(a,M=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ M=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\left(\sqrt{x}-1\right)\\ M=\dfrac{x-1}{\sqrt{x}}\\ b,M>0\Leftrightarrow x-1>0\left(\sqrt{x}>0\right)\\ \Leftrightarrow x>1\)
Bài 10:
\(a,A=\dfrac{\sqrt{\left(x+3\right)^2}}{x+3}=\dfrac{\left|x+3\right|}{x+3}\)
Với \(x\ge-3\Leftrightarrow A=\dfrac{x+3}{x+3}=1\)
Với \(x< -3\Leftrightarrow A=\dfrac{-\left(x+3\right)}{x+3}=-1\)
\(b,B=\dfrac{2}{x-1}\cdot\dfrac{\left|x-1\right|}{2\left|x\right|}\)
Với \(0< x< 1\Leftrightarrow B=\dfrac{2}{x-1}\cdot\dfrac{-\left(x-1\right)}{2x}=-\dfrac{1}{x}\)

\(13,=\dfrac{\sqrt{3}\left(\sqrt{6}-2\right)}{\sqrt{6}-2}+\dfrac{4\left(\sqrt{3}-1\right)}{2}+12-3\sqrt{3}\\ =\sqrt{3}+2\sqrt{3}-2+12-3\sqrt{3}=10\\ 14,=\dfrac{12\left(4+\sqrt{10}\right)}{6}-3\sqrt{10}+\dfrac{\sqrt{10}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\\ =8+2\sqrt{10}-3\sqrt{10}+\sqrt{10}=8\\ 15,=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{-3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{-3}{\sqrt{x}-3}\)
\(16,=\dfrac{x+2\sqrt{x}-3-x+3\sqrt{x}-4\sqrt{x}-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ 17,=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)


2.1
ĐKXĐ: \(x\ge-\dfrac{1}{16}\)
\(x^2-x-20-2\left(\sqrt{16x+1}-9\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)-\dfrac{32\left(x-5\right)}{\sqrt{16x+1}+9}=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4-\dfrac{32}{\sqrt{16x+1}+9}\right)=0\) (1)
Do \(x\ge-\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}\dfrac{32}{\sqrt{16x+1}+9}< \dfrac{32}{9}\\x+4\ge-\dfrac{1}{16}+4=\dfrac{63}{16}>\dfrac{32}{9}\end{matrix}\right.\)
\(\Rightarrow x+4-\dfrac{32}{\sqrt{16x+1}+9}>0\)
Nên (1) tương đương:
\(x-5=0\)
\(\Leftrightarrow x=5\)
Câu 2.2, 2.3 đề lỗi không dịch được






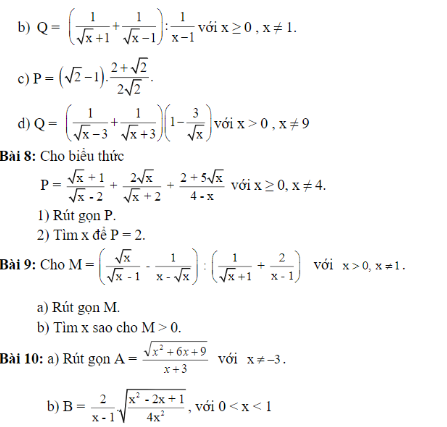




Bài 2.
ĐKXĐ của biểu thức đã cho là:
\(\hept{\begin{cases}x\ge0,\sqrt{x}\ne0\\\sqrt{x}-1\ne0\\\sqrt{x}-2\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x>0\\x\ne1,x\ne2\end{cases}}\).
\(A=\left(\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}}\right)\div\left(\frac{\sqrt{x}+1}{\sqrt{x}-2}-\frac{\sqrt{x}+2}{\sqrt{x}-1}\right)\)
\(=\frac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\div\left[\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}-\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\right]\)
\(=\frac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\div\left(\frac{x-1-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\frac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)=\frac{\sqrt{x}-2}{\sqrt{x}}\)
\(A>\frac{1}{6}\Rightarrow\frac{\sqrt{x}-2}{\sqrt{x}}>\frac{1}{6}\Leftrightarrow6\left(\sqrt{x}-2\right)>\sqrt{x}\)
\(\Leftrightarrow5\sqrt{x}>12\Leftrightarrow x>\frac{144}{25}\).