Question

[Vinh Thuy Duong]

Bài 2: Cho tam giác ABC cân tại A, M là điểm bấy kì nằm giữa hai điểm A và B. Trên tia đối của tia CA lấy N sao cho CN=BM. Vẽ ME và NF lần lượt vuông góc với đường thẳng BC. Gọi I là giao điểm của MN và BC.

a) Chứng minh rằng: IE =IF

b) Trên cạnh AC lấy D sao cho CD =CN. Chứng minh rằng BMDC là hình thang cân. 

Answer 1

[Nguyễn Lê Phước Thịnh]

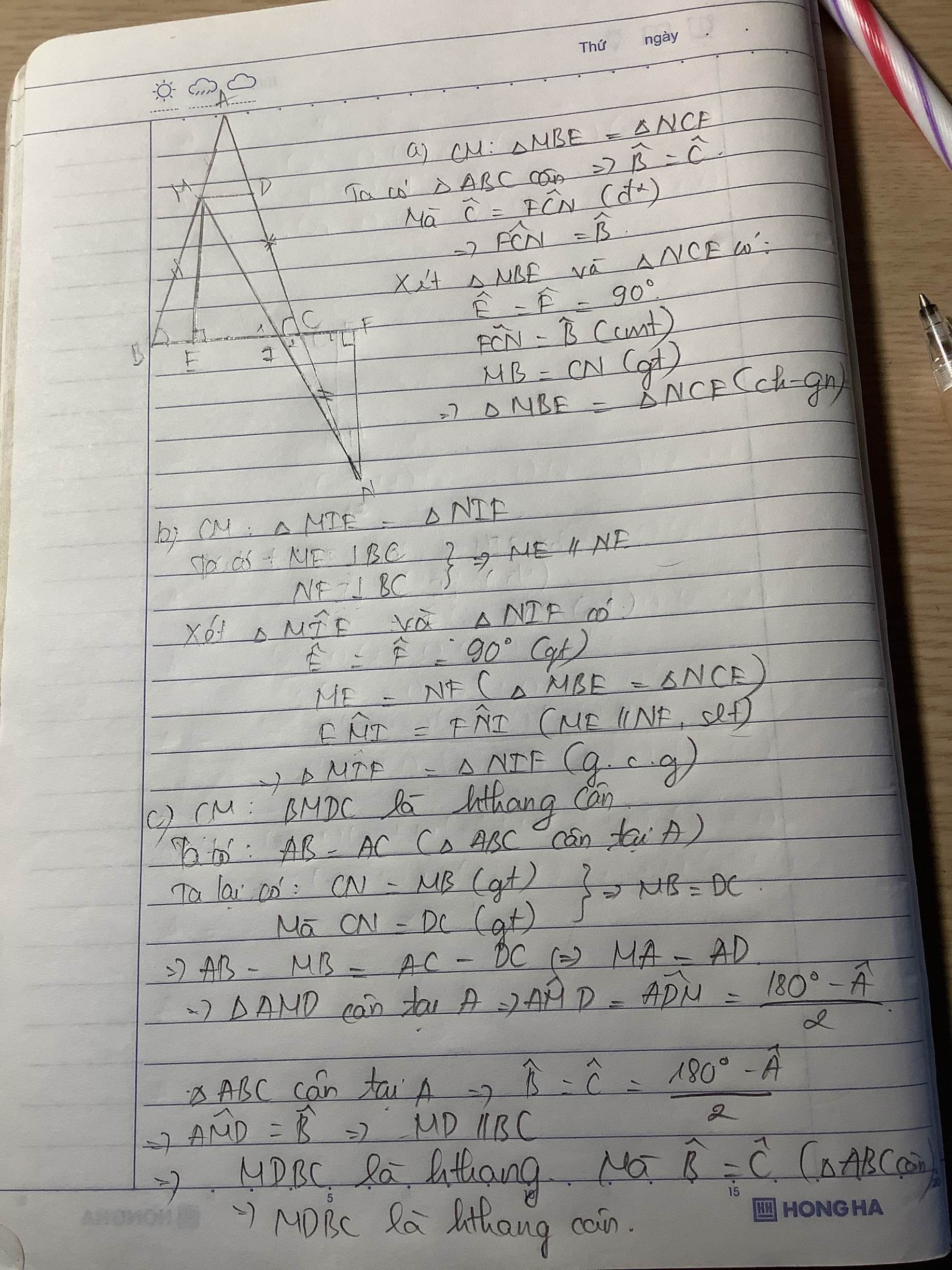
a: Xét ΔMBE vuông tại E và ΔNCF vuông tại F có

MB=CN

\(\widehat{MBE}=\widehat{NCF}\left(=\widehat{ACB}\right)\)

Do đó: ΔMBE=ΔNCF

Suy ra: ME=NF

Xét ΔMEI vuông tại E và ΔNFI vuông tại F có

ME=NF

\(\widehat{EMI}=\widehat{FNI}\)

Do đó: ΔMEI=ΔNFI\(\left(cgv-gnk\right)\)

Suy ra: IE=IF

b: Ta có: CD=CN

mà CN=MB

nên MB=DC

Xét ΔBAC có 

\(\dfrac{MB}{BA}=\dfrac{CD}{AC}\)

nên MD//BC

Xét tứ giác BMDC có MD//BC

nên BMDC là hình thang

mà \(\widehat{MBC}=\widehat{DCB}\)

nên BMDC là hình thang cân