Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

PMNIEFKH
a) Xét \(\Delta PIM;\Delta PIN\) có :
\(PM=PN\) (tam giác MNP cân tại P)
\(\widehat{MPI}=\widehat{NPI}\) (PI là tia phân giác của \(\widehat{MPN}\) )
\(PI:chung\)
=> \(\Delta PIM=\Delta PIN\left(c.g.c\right)\)
*Cách khác :
Xét \(\Delta PIM;\Delta PIN\) có :
\(\widehat{PMI}=\widehat{PNI}\) (tam giác MNP cân tại P)
\(PM=PN\)(tam giác MNP cân tại P)
\(\widehat{MPI}=\widehat{NPI}\) (PI là tia phân giác của góc MPN)
=> \(\Delta PIM=\Delta PIN\left(g.c.g\right)\)
b) Xét \(\Delta PEI;\Delta PFI\) có :
\(\widehat{PEI}=\widehat{PFI}\left(=90^{^O}\right)\)
\(PI:Chung\)
\(\widehat{EPI}=\widehat{FPI}\left(cmt\right)\)
=> \(\Delta PEI=\Delta PFI\) (cạnh huyền - góc nhọn)
=> \(IE=IF\) (2 cạnh tương ứng)
c) Ta chứng minh được \(\Delta PIK=\Delta PIH\left(g.c.g\right)\)
Suy ra : \(PK=PH\) (2 cạnh tương ứng)
Xét \(\Delta PHK\) có :
\(PK=PH\left(cmt\right)\)
=> \(\Delta PHK\) cân tại P (đpcm)
d) Xét \(\Delta PEF\) cân tại E có :
\(\widehat{PEF}=\widehat{PFE}=\dfrac{180^o-\widehat{P}}{2}\left(1\right)\)
Xét \(\Delta PKH\) cân tại P (cmt) có :
\(\widehat{PKH}=\widehat{PHK}=\dfrac{180^o-\widehat{P}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{PEF}=\widehat{PKH}\left(=\dfrac{180^o-\widehat{P}}{2}\right)\)
Mà thấy : 2 góc này đều ở vị trí đồng vị
=> \(\text{EF // HK (đpcm)}\)

M N P C A I
a) Xét \(\Delta PAM;\Delta PCN\) có :
\(\widehat{PAM}=\widehat{PCN}\left(=90^{^O}\right)\)
\(PM=PN\) (Tam giác MNP cân tại P)
\(\widehat{P}:Chung\)
=> \(\Delta PAM=\Delta PCN\)(cạnh huyền - góc nhọn)
=> \(PA=PC\) (2 cạnh tương ứng)
* Mình sửa lại chút nhé , chứng minh CA // MN (có gì sai sót thì bạn góp ý nhé)
Xét \(\Delta PCA\) cân tại P (PA =PC - cmt) có :
\(\widehat{PCA}=\widehat{PAC}=\dfrac{180^o-\widehat{P}}{2}\left(1\right)\)
Xét \(\Delta PMN\) cân tại P có :
\(\widehat{PMN}=\widehat{PNM}=\dfrac{180^o-\widehat{P}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{PCA}=\widehat{PMN}\left(=\dfrac{180^o-\widehat{P}}{2}\right)\)
Mà thấy : 2 góc này ở vị trí đồng vị
Suy ra : CA // MN (đpcm)
b) Xét \(\Delta CMN;\Delta AMN\) có:
\(\widehat{CMN}=\widehat{ANM}\) (tam giác MPN cân tại P)
\(MN:chung\)
\(\widehat{MCN}=\widehat{NAM}\left(=90^o\right)\)
=> \(\Delta CMN=\Delta AMN\) (cạnh huyền - góc nhọn)
=> \(\widehat{CNM}=\widehat{AMN}\) (2 góc tương ứng)
Xét \(\Delta IMN\) có :
\(\widehat{IMN}=\widehat{INM}\) (do \(\widehat{CNM}=\widehat{AMN}\)- cmt)
=> \(\Delta IMN\) cân tại I (đpcm)
c) Xét \(\Delta PMK;\Delta PNK\) có :
\(PM=PN\left(gt\right)\)
\(\widehat{PMK}=\widehat{PNK}\) (Tam giác MNP cân tại P)
\(PK:chung\)
=> \(\Delta PMK=\Delta PNK\left(c.g.c\right)\)
=> \(MK=NK\) (2 cạnh tương ứng)
Do đó : K là trung điểm của MN

a) Có △MNP cân tại M
\(\Rightarrow\left\{{}\begin{matrix}MN=MP\\\widehat{MNP}=\widehat{MPN}\end{matrix}\right.\)
\(MH\perp NP\Rightarrow\widehat{MHN}=\widehat{MHP}=90^o\)
Xét △MHN và △MHP có:
\(\widehat{MHN}=\widehat{MHP}=90^o\\ MN=MP\\ \widehat{MNH}=\widehat{MPH}\)
\(\Rightarrow\text{△MHN = △MHP}\left(\text{cạnh huyền - góc nhọn}\right)\)
\(\Rightarrow HN=HP\) (2 cạnh tương ứng)
Mà H ∈ NP
\(\Rightarrow\) H là trung điểm của NP
b) \(HD\perp MN\Rightarrow\widehat{HDM}=\widehat{HDN}=90^o\\ HE\perp MP\Rightarrow\widehat{HEM}=\widehat{HEP}=90^o \)
Xét △HDN và △HEP có:
\(\widehat{HDN}=\widehat{HEP}=90^o\\ HN=HP\\ \widehat{DNH}=\widehat{EPH}\)
\(\Rightarrow\text{△HDN = △HEP}\left(\text{cạnh huyền - góc nhọn}\right)\)
\(\Rightarrow HD=HE\) (2 cạnh tương ứng)
Xét △HDE có HD = HE
\(\Rightarrow\) △HDE cân tại H
c) Có △HDN = △HEP
\(\Rightarrow DN=EP\) (2 cạnh tương ứng)
Mà MN = MP
\(\Rightarrow MD=ME\)
Xét △MDE có MD = ME
\(\Rightarrow\) △MDE cân tại M
\(\Rightarrow\widehat{MDE}=\frac{180^o-\widehat{NMP}}{2}\left(1\right)\)
Lại có: △MNP cân tại M
\(\Rightarrow\widehat{MNP}=\frac{180^o-\widehat{NMP}}{2}\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\widehat{MDE}=\widehat{MNP}\)
Mà 2 góc ở vị trí đồng vị
\(\Rightarrow\) DE // NP (dấu hiệu nhận biết)
Mà \(MH\perp NP\)
\(\Rightarrow DE\perp MH\) (quan hệ từ vuông góc đến song song)
a) Xét ΔMHN vuông tại H và ΔMHP vuông tại H có
MN=MP(do ΔMNP cân tại M)
MH là cạnh chung
Do đó: ΔMHN=ΔMHP(cạnh huyền-cạnh góc vuông)
⇒NH=HP(hai cạnh tương ứng)
mà H∈NP(gt)
nên H là trung điểm của NP(đpcm)
b)Xét ΔDHN vuông tại D và ΔEHP vuông tại E có
NH=HP(cmt)
\(\widehat{DNH}=\widehat{EPH}\)(hai góc ở đáy của ΔMNP cân tại M)
Do đó: ΔDNH=ΔEPH(cạnh huyền-góc nhọn)
⇒DH=EH(hai cạnh tương ứng)
Xét ΔHDE có DH=EH(cmt)
nên ΔHDE cân tại H(đpcm)
c)Gọi O là giao điểm của DE và MH
Ta có: \(\widehat{NDH}+\widehat{HDO}+\widehat{MDO}=180độ\)
\(\widehat{PEH}+\widehat{OEH}+\widehat{MEO}=180độ\)
mà \(\widehat{NDH}=\widehat{HEP}\)(=90 độ)
và \(\widehat{HDO}=\widehat{OEH}\)(ΔHDE cân tại H)
nên \(\widehat{MDO}=\widehat{MEO}\)
hay \(\widehat{MDE}=\widehat{MED}\)(vì O∈ED)
Xét ΔMDE có \(\widehat{MDE}=\widehat{MED}\)(cmt)
nên ΔMDE cân tại M(định lí đảo của tam giác cân)
Ta có: ΔMHN=ΔMHP(cmt)
\(\Rightarrow\widehat{NMH}=\widehat{PMH}\)(hai góc tương ứng)
mà D∈MN(gt)
và E∈MP(gt) và O∈MH(theo cách gọi)
nên \(\widehat{DMO}=\widehat{EMO}\)
Xét ΔMDO và ΔMEO có
MD=ME(ΔMDE cân tại M)
\(\widehat{DMO}=\widehat{EMO}\)(cmt)
MO là cạnh chung
Do đó: ΔMDO=ΔMEO(c-g-c)
⇒\(\widehat{MOD}=\widehat{MOE}\)(hai góc tương ứng)
mà \(\widehat{MOD}+\widehat{MOE}=180độ\)(do D,O,E thẳng hàng)
nên \(\widehat{MOD}=\widehat{MOE}=\frac{180độ}{2}=90độ\)
⇒MO⊥DE
hay MH⊥DE(đpcm)

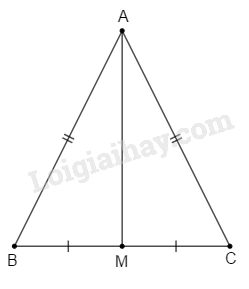
Xét \(\Delta ABC\) có:
c) Ta có \(\Delta ABC\) cân tại \(A\left(cmt\right).\)
=> \(\widehat{B}=\widehat{C}\) (tính chất tam giác cân).
Xét 2 \(\Delta\) vuông \(HBM\) và \(KCM\) có:
\(\widehat{MHB}=\widehat{MKC}=90^0\left(gt\right)\)
\(BM=CM\) (như ở trên)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
=> \(\Delta HBM=\Delta KCM\) (cạnh huyền - góc nhọn).
=> \(HM=KM\) (2 cạnh tương ứng).
Chúc bạn học tốt!

Bài 3:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{3}{2}}=\dfrac{b}{\dfrac{4}{3}}=\dfrac{c}{\dfrac{5}{4}}=\dfrac{a+b+c}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{196}{\dfrac{49}{12}}=48\)
Do đó: a=72; b=64; c=60
