Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vì AB, AC là các tiếp tuyến của (O) nên AB=AC ⇒ ΔABC cân tại A.
Ta có AO là đường phân giác của góc ∠BAC của tam giác cân ABC nên AO cũng là đường cao.Suy ra OA ⊥ BC (tính chất của tam giác cân).
b) Gọi I là giao điểm của AO với BC
Ta có: ΔIBA = ΔICA (Cạnh huyền góc nhọn)
⇒IB = IC
Trong ΔBCD ta có:
IB = ID
OC = OD
⇒ OI là đường trung bình của Δ BCD
Nên OI//BD hay AO//BD
Vậy AO//BD(đpcm)
c) Vì AB là tiếp tuyển của (O) với B là tiếp điểm nên AB ⊥ OB và AB = AC
Vậy ΔOAB vuông tại B.
Áp dụng định lí Pytago trong tam giác vuông OAB, ta có:
AO2 = AB2 + BO2
⇒ AB2 = AO2 – BO2 = 42 -22 = 12
⇒ AB = √12 = 2√3 (cm)
- Trong tam giác vuông OAB ta có
sinOAB = OB/OA =2/4 = 1/2
⇒ ∠OAB = 300 ⇒∠BAC = 2∠OAB =2.300 = 600
Tam giác ABC cân tại A và có ∠A = 600 nên ΔABC là tam giác đều. Suy ra AB= BC = CA = 2√3 (cm)
Nhận xét. Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng 600.

a) Vì AB, AC là các tiếp tuyến nên AB=AC và ˆA1=ˆA2A1^=A2^.
Suy ra OA⊥BCOA⊥BC (tính chất của tam giác cân).
b) Điểm B nằm trên đường tròn đường kính CD nên ˆCBD=90∘CBD^=90∘.
Suy ra BD//AO (vì cùng vuông góc với BC).
c) Nối OB thì OB⊥AB.OB⊥AB.
Xét tam giác AOB vuông tại B có:\(\sin A_1=\dfrac{OA}{OB}=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\Rightarrow\widehat{A_1}=30^O\Rightarrow\widehat{BAC}=60^O\)
Tam giác ABC cân, có một góc 60\(^o\) nên là tam giác đều.
Ta có AB\(^2\)=OA\(^2\)−OB\(^2\)=4\(^2\)−2\(^2\)=12⇒AB=\(2\sqrt{3}\).
Vậy AB=AC=BC=\(2\sqrt{3}cm\)
Nhận xét. Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng 60\(^O\)

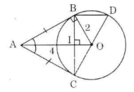
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD // HO (HO là đường trung bình của BCD) ⇒ BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
A C 2 = O A 2 – O C 2 = 4 2 – 2 2 = 12
=> AC = √12 = 2√3 (cm)
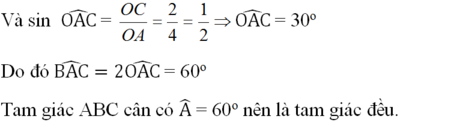
Do đó AB = BC = AC = 2√3 (cm).

Bạn tự vẽ hình nha
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD // OI (OI là đường trung bình của tam giác BCD).
Vậy BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
AC^2 = OA^2 – OC^2 = 42 – 22 = 12
=> AC = √12 = 2√3 (cm)
\(\sin OAC=\frac{OC}{OA}=\frac{1}{2}\)
=> OAC =30 độ
mà BAC =2OAC
=. BAC =60
Tam giác ABC cân có BAC = 60 => Tam giác ABC đều
+> AB=AC=BC=2√3 (cm)
K cho mk nh
câu A : AB = AC ( theo tính chất của đường tiếp tuyến ) suy ra : tam giác ABC cân tại A , OA là đường phân giác cũng là đường cao vậy OA vuông góc với BC

4 2 A B C D O I
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên \(\Delta ABC\) cân tại A.
Lại có AO là tia phân giác của góc A nên \(AO\perp BC\) (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét tam giác CBD có :
CI = IB
CO = OD (bán kính)
=> BD // HO (HO là đường trung bình của BCD) => BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
AC2 = OA2 – OC2 = 42 – 22 = 12
\(\Rightarrow AC=\sqrt{12}=2\sqrt{3}\left(cm\right)\)
Và \(\sin\widehat{OAC}=\frac{OC}{OA}=\frac{2}{4}=\frac{1}{2}\Rightarrow=\widehat{OAC}=30^o\)
Do đó \(\widehat{BAC}=2\widehat{OAC}=60^o\)
Tam giác ABC cân có \(\widehat{A}=60^o\)nên là tam giác đều
Do đó : \(AB=BC=AC=2\sqrt{3}\left(cm\right)\)

AB = AC và OB = OC nên OA là trung trực của đoạn BC, do đó OA vuông góc với BCbot BC.
b) Chứng minh được BC \bot⊥ BD nên BD // AO.
c) Tam giác vuông ABO có \cos O = \dfrac12cosO=21 nên \widehat{O} = 60^\circO=60∘.
Từ đó chứng minh được tam giác ABCABC đều, AB = AO.\sin 60\degree = 4.\dfrac{\sqrt3}{2} = 2\sqrt3AB=AO.sin60°=4.23=23 cm.
a) AB = AC và OB = OC nên OA là trung trực của đoạn BC, do đó OA botbot BC.
b) Chứng minh được BC ⊥⊥ BD nên BD // AO.
c) Tam giác vuông ABO có cosO=12cosO=12 nên ˆO=60∘O^=60∘.
Từ đó chứng minh được tam giác ABCABC đều, AB=AO.sin60\degree=4.√32=2√3AB=AO.sin60\degree=4.32=23 cm
Bài 2:
a) Ta thấy:
$6^2+4,5^2=7,5^2\Leftrightarrow AB^2+AC^2=BC^2$
Theo định lý Pitago đảo ta suy ra $ABC$ là tam giác vuông tại $A$
b)
$S_{ABC}=\frac{AB.AC}{2}=\frac{AH.BC}{2}$
$\Rightarrow AH=\frac{AB.AC}{BC}=\frac{6.4,5}{7,5}=3,6$ (cm)
$\sin B=\frac{AC}{BC}=\frac{4,5}{7,5}\Rightarrow \widehat{B}\approx 36,8^0$
$\Rightarrow \widehat{C}\approx 90^0-36,78^0=53,2^0$
Hình 2: