Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAHB vuông tại H và ΔAHD vuông tại H có
HB=HD
AH chung
Do đó: ΔAHB=ΔAHD
Suy ra: AB=AD
Xét ΔABD có AB=AD
nên ΔABD cân tại A
b: Xét ΔCHB vuông tại H và ΔCHD vuông tại H có
CH chung
HB=HD
Do đó: ΔCHB=ΔCHD
Suy ra: CB=CD
c: Xét ΔDBC có
BM là đường cao ứng với cạnh DC
CH là đường cao ứng với cạnh BD
BM cắt CH tại I
Do đó: I là trực tâm của ΔDCB
Suy ra: DI\(\perp\)BC

a) ABC cân tại A (gt) => AB=AC và góc ABC = góc ACB
=> góc ABM = góc ACN ( các góc kề bù với góc ABC và góc ACB)
Xét tam giác ABM và tam giác ACN có
AB=AC
góc ABM= góc ACN (cmt)
BM=CN )gt)
=> tam giác ABM = tam giác ACN ( c.g.c)
=> AM=AN ( 2 cạnh tương ứng)
b) tam giác ABM = tam giác ACN (cmt)
=> góc M= góc N (cặp góc tương ứng)
Xét tam giác HBM và tam giác KCN có
góc BHM= góc CKN =90 độ (BH vuông góc AM, AN vuông góc CK)
BM = CN (Gt)
góc M= góc N (cmt)
=> tam giác HBM = tam giác KCN ( cạnh huyền - góc nhọn)
c) TA có tam giác HBC và tam giác KCN (cmt)
=> góc HBM = góc KCN (hai goc tương ứng)
MÀ góc HBM = góc CBO ( hai góc đối đỉnh )
góc KCN=góc BCO ( hai góc đối đỉnh )
=> góc CBO= góc BCO
=> tam giác OBC cân tại O ( dấu hiệu nhận biết tam giác vuông)

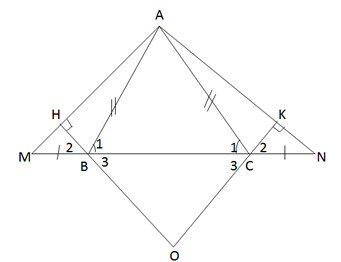
a) ∆ABC cân, suy ra ˆB1=ˆC1B1^=C1^
⇒ˆABM=ˆACN⇒ABM^=ACN^
∆ABM và ∆CAN có:
AB = AC (gt)
ˆABM=ˆACNABM^=ACN^
BM = ON (gt)
Suy ra ˆM=ˆNM^=N^
=>∆AMN là tam giác cân ở A.
b) Hai tam giác vuông ∆BHM và ∆CKN có :
BM = CN (gt)
ˆM=ˆNM^=N^ (CM từ câu a)
Nên ∆BHM = ∆CHN (cạnh huyền, góc nhọn)
Suy ra BH = CK.
c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*)
Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**).
Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK
Vậy AH = AK.
d) ∆BHM = ∆CKN suy ra ˆB2=ˆC2B2^=C2^
Mà ˆB2=ˆB3;ˆC2=ˆC3B2^=B3^;C2^=C3^ (đối đỉnh)
Nên ˆB3=ˆC3B3^=C3^ .
Vậy ∆OBC là tam giác cân.
e) Khi ˆBAC=600BAC^=600 và BM = CN = BC.
+Tam giác cân ABC có ˆBAC=600BAC^=600 nên là tam giác đều.
Do đó: AB = BC = AC = BM = CN
ˆABM=ˆACN=1200ABM^=ACN^=1200 (cùng bù với 600)
∆ABM cân ở B nên ˆM=ˆBAM=1800–12002=300M^=BAM^=1800–12002=300 .
Suy ra ˆANM=ˆAMN=300ANM^=AMN^=300 .
Và ˆMAN=1800–(ˆAMN+ˆANM)=1800–2.300=1200MAN^=1800–(AMN^+ANM^)=1800–2.300=1200
Vậy ∆AMN có ˆM=ˆN=300;ˆA=1200.M^=N^=300;A^=1200.
+∆BHM có: ˆM=300M^=300 nên ˆB2=600B2^=600 (hai góc phụ nhau)
Suy ra ˆB3=600B3^=600
Tương tự ˆC3=600C3^=600
Tam giác OBC có ˆB3=ˆC3=600B3^=C3^=600 nên tam giác OBC là tam giác đều.
(Tam giác cân có một góc bằng 600 nên là tam giác đều).

a) xét tam giác ABH và tam giác ACH có
Góc AHB =Góc AHC =90 độ
AB =AC ( do tam giác abc cân)
Góc B = góc C (do tam giác abc cân)
=> tam giác ABH = tam giác ACH ( cạnh huyền, góc nhọn)
=>HB= HC (hai cạnh tương ứng bằng nhau)
b) Xét tam giác MAK và tam giác MCK có
AK=KH( gì)
Góc AKB = GÓC CKB=90 độ
MK chung
=>tam giác MAK = tam giác MCK( c. g. c)
=> MA=CM( hai cạnh tương ứng)
c) từ tam giác mak = tam giác MCK ( câu b)
=>góc MAK = góc C (..)
TA CÓ tam giác abc cân ở A =>góc B = góc C
=>góc Abc = góc Mak
d) cậu xem lại đề phần này đi nha mik thấy nó sai cái j đó
a: Xét ΔABH vuông tại H và ΔADH vuông tại H có
AH chung
HB=HD
Do đó: ΔABH=ΔADH
Suy ra: AB=AD
hay ΔABD cân tại A
b: Xét ΔCBH vuông tại H và ΔCDH vuông tại H có
CH chung
BH=DH
Do đó: ΔCBH=ΔCDH
Suy ra: CB=CD
c:Xét ΔBDC có
BM là đường cao ứng với cạnh DC
CH là đường cao ứng với cạnh BD
BM cắt CH tại I
Do đó: I là trực tâm của ΔBDC
Suy ra: DI\(\perp\)BC