Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
17)\(AH^2=\frac{3b^2}{4};\Delta BCD;AD=b-\frac{a^2}{b}\)
MÀ \(AD^2=AH^2+DH^2=b^2-ab+a^2\)
Bài 1:
Ta có:góc ABD=góc CBD
góc ECB=góc AEC
Mà góc B = góc C
suy ra góc ABD = góc CBD = góc ECB=gócACE
Ta lại có:góc B = góc C
=> BEDC là hình thang cân=>BC//DE
=>BE=DCvà BD=CE
Mà tam giác ABC cân tại A=>AE=AD
Vì góc DBC= góc EDB(so le trong)
Mà ABD=DBC=>góc ABD= góc DBC=>tam giác EBD cân tai E
=>EB=EDmà EB=DC
=>ED=EB=DC.đpcm
Bài 2:
Ta có :
góc ACD=góc BDC
=>ABCD là HTC(định nghĩa hình thang cân)
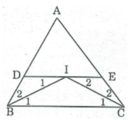
DE // BC (theo cách vẽ)
⇒ ∠ I 1 = ∠ B 1 (hai góc so le trong)
Mà ∠ B 1 = ∠ B 2 (gt)
Suy ra: ∠ I 1 = ∠ B 2
Do đó: ∆ BDI cân tại D ⇒ DI = DB (1)
Ta có: ∠ I 2 = ∠ C 1 (so le trong)
∠ C 1 = ∠ C 2 (gt)
Suy ra: ∠ I 2 = ∠ C 2 do đó: ∆ CEI cân tại E
⇒ IE = EC (2)
DE = DI + IE (3)
Từ (1), (2), (3) suy ra: DE = BD + CE
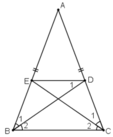
- Chứng minh tứ giác BCDE là hình thang cân:
+ ΔABC cân tại A 
BD là phân giác của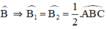 
CE là phân giác của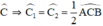 
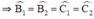
+ Xét ΔAEC và ΔADB có:
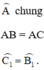
⇒ ΔAEC = ΔADB
⇒ AE = AD
Vậy tam giác ABC cân tại A có AE = AD
Theo kết quả bài 15a) suy ra BCDE là hình thang cân.
- Chứng minh ED = EB.
ED // BC ⇒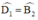 
(Hai góc so le trong)
Mà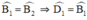 
⇒ ΔEDB cân tại E ⇒ ED = EB.
Vậy ta có EBCD là hình thang cân có đáy nhỏ bằng cạnh bên.
a: AE/BC=AE/AB=5,6/16=7/20
AD/AC=3,5/10=7/20
=>AE/AB=AD/AC
=>ΔAED đồg dạng với ΔABC
b: ΔAED đồng dạng với ΔABC
=>DE/BC=AE/AB
=>DE/16=7/20
=>DE=5,6cm
Xét ΔABC có
BD là đường phân giác ứng với cạnh AC
nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(1\right)\)
Xét ΔABC có
CE là đường phân giác ứng với cạnh AB
nên \(\dfrac{AE}{EB}=\dfrac{AC}{BC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AE}{EB}=\dfrac{AD}{DC}\)
hay DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
Suy ra: EB=DC(3)
Xét ΔEDB có \(\widehat{EBD}=\widehat{EDB}\left(=\widehat{DBC}\right)\)
nên ΔEDB cân tại E
Suy ra: EB=ED(4)
Từ (3) và (4) suy ra EB=ED=DC
mình biết đấy
đề hơi sai chỉnh lại nha mọi ngừi Bài 17. Cho tam giác ABC (AB=AC) có góc ở đỉnh bằng 20 độ; cạnh đáy là a ; cạnh bên là b . Chứng minh rằng a3 + b3 = 3ab2