Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AHBC có
E là trung điểm chung của AB và HC
=>AHBC là hình bình hành
Xét tứ giác ABCK có
D là trung điểm chung của AC và BK
=>ABCK là hình bình hành
b: Ta có: AHBC là hình bình hành
=>AH//BC và AH=BC
Ta có: ABCK là hình bình hành
=>AK//BC và AK=BC
Ta có: AH//BC
AK//BC
HA,AK có điểm chung là A
Do đó: H,A,K thẳng hàng
Ta có: AH=BC
AK=BC
Do đó: AH=AK
mà H,A,K thẳng hàng
nên A là trung điểm của HK

Bài 1:
a: Xét tứ giác AHBC có
E la trung điểm chung của AB và CH
=>AHBC là hình bình hành
Xét tứ giác AKCB có
D là trung điểm chung của AC va KB
=>AKCB là hình bình hành
b: AHBC là hinh bình hanh
=>AH//BC và AH=BC
AKCB là hình bình hành
=>AK//BC và AK=BC
ta có: AH//BC
AK//BC
mà AH,AK có điểm chung là A
nên H,A,K thẳng hàng
Ta có: AK=BC
AH=BC
Do đó: AK=AH
mà H,A,K thẳng hàng
nên A là trung điểm của HK
Bài 2:
a: Ta có; AE+DE=AD
CF+FB=CB
ma AE=CF và AD=BC
nên DE=BF
Ta có: AM+MB=AB
CN+ND=CD
ma MB=ND va AB=CD
nên AM=CN
Xét ΔEAM và ΔFCN có
EA=FC
\(\hat{EAM}=\hat{FCN}\) (ABCD là hình bình hành)
AM=CN
Do đó: ΔEAM=ΔFCN
=>EM=FN
Xét ΔEDN và ΔFBM có
ED=FB
\(\hat{EDN}=\hat{FBM}\) (ABCD là hình bình hành)
DN=BM
Do đó: ΔEDN=ΔFBM
=>EN=FM
Xét tứ giác EMFN có
EM=FN
EN=FM
Do đó: EMFN là hình bình hành
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường(1)
ta có: EMFN là hình binh hành
=>EF cắt MN tại trung điểm của mỗi đường(2)
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(3)
Từ (1),(2),(3) suy ra AC,EF,BD,MN đồng quy

Bài 2:
A C D B E H K
Dễ dàng chứng minh \(\Delta\)BEC = \(\Delta\)AEH (c.g.c) và \(\Delta\)CDB = \(\Delta\)ADK
Suy ra HA = BC. và KA = BC từ đó suy ra HA = KA (1)
Do ED là đường trung bình tam giác BAK nên ED // AK (2)
Do ED là đường trung bình tam giác HCA nên ED // AH (3)
Từ (2) và (3) theo tiên đề Ơclit suy ra A, H, K thẳng hàng (4)
Từ (1) và (4) suy ra đpcm.
Bài 1:
A B C M K H
Hình như hơi dư thừa nhỉ? BHCK là hình bình hành thì hiển nhiên CH//BK rồi mà. Đúng hay sai thì tùy!
Giải
Dễ dàng chứng minh \(\Delta\)BMH = \(\Delta\)CMK (cạnh huyền - góc nhọn)
Suy ra ^MBH = ^MCK. Mà hai góc này ở vị trị so le trong nên BH // CK (1) và MH = MK
Xét \(\Delta\)BMK và \(\Delta\)CMH có:
MH = MK (chứng minh trên)
^BMK = ^HMC
BM = CM (do M là trung điểm BC)
Suy ra \(\Delta\)BMK = \(\Delta\)CMH (c.g.c)
Suy ra ^MBK = ^MCH. Mà hai góc này ở vị trí so le trong nên BK // CH (2)
Từ (1) và (2) suy ra tứ giác BHCK là hình bình hành (đpcm)

xét tg HAE và tg CEB:
HE=EC ( gt )
AE=EB (gt )
góc HEA=góc BEC ( đối đỉnh )
=> tg HAE= tg CEB ( c-g-c )
=> HA=BC ( 2 cạnh tương ứng ) ( 1)
=> góc HAE=góc EBC ( 2 góc tương ứng ) (2)
xét tương tự tg AKD và tg CBD ( tự chứng minh 2 tg bằng nhau)
=> AK= BC ( 2 cạnh tương ứng ) ( 3)
=> góc KAD= góc DCB ( 2 cạnh tương ứng ) ( 4)
từ (1) và (2) => HA=AK ( * )
từ (3) và (4 ) => góc HAE + góc BAC = góc KAD = góc ACB + góc ABC + góc BAC = 180 độ ( tổng 3 góc trog hình tg )
=> H,A,K thẳng hàng ( ** )
từ ( *) và ( ** ) => A là tđ của HK

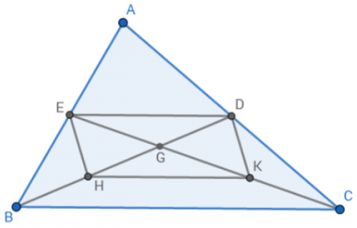
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi


a: Xét tứ giác AHBC có
E là trung điểm chung của AB và HC
=>AHBC là hình bình hành
Xét tứ giác AKCB có
D là trung điểm chung của AC và KB
=>AKCB là hình bình hành
b:AHBC là hình bình hành
=>AH//BC và AH=BC
AKCB là hình bình hành
=>AK//CB và AK=CB
AH//BC
AK//BC
mà AH,AK có điểm chung là A
nên H,A,K thẳng hàng
AH=BC
AK=BC
Do đó: AH=AK
H,A,K thẳng hàng
mà AH=AK
nên A là trung điểm của HK