K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
Các bạn giải giúp mình bài 4 và bài 5 phần Tự luận nhé
2
15 tháng 11 2021
a)
Ta thấy ACB=50 độ
CBE=50 độ
Mà 2 góc này là 2 góc so le trong
=>a // b (đpcm)
b)Ta thấy:
AB ⊥ a mà a // b
=>AB ⊥ b (Từ vuông góc đến song song) (đpcm)
c)Ta có:
DBE+BED+BDE=180 độ (Tổng 3 góc trong tam giác)
=>BDE=180-DBE-BED=180-50-40=90 độ
Mà BDE+CDE=180 độ (2 góc kề bù)
=>CDE=180-BDE=180-90=90 độ
Vậy CDE=90 độ
1 tháng 7 2023
1:
a: Bảng tần số:
| Điểm số | 7 | 8 | 9 | 10 |
| tần số | 3 | 2 | 1 | 4 |
b: Trung bình cộng là:
\(\dfrac{7\cdot3+8\cdot2+9+10\cdot4}{10}=8.6\)
23 tháng 10 2021
Bài 2:
\(c,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{x-y}{6-5}=\dfrac{-28}{1}=-28\\ \Leftrightarrow\left\{{}\begin{matrix}x=-28\cdot6=-168\\y=-28\cdot5=-140\end{matrix}\right.\)
Bài 3:
a, Vì \(\widehat{ABC}=60^0=20^0+40^0=\widehat{BCE}+\widehat{CED}=\widehat{BCD}\) mà 2 góc này ở vị trí slt nên AB//CD
Vì \(\widehat{ECD}+\widehat{CEF}=140^0+40^0=180^0\) mà 2 góc này ở vị tri tcp nên CD//EF
Do đó AB//EF (//CD)
b, Vì Ex là p/g nên \(\widehat{CEM}=\dfrac{1}{2}\widehat{CEF}=70^0\)
Xét tg CEM có \(\widehat{EMC}=180^0-\widehat{CEM}-\widehat{ECM}=180^0-70^0-40^0=70^0\)
19 tháng 1 2023
Câu 4:
a: Xét ΔIAM và ΔIEB có
góc IAM=góc IEB
IE=IA
góc AIM=góc EIB
Do đo: ΔIAM=ΔIEB
=>AM=BE
b: ΔAIM=ΔEIB
=>IB=IM
=>I là trung điểm của BM
Xét tứ giác ANEC có
I là trung điểm chung của AE và NC
nên ANEC là hình bình hành
=>AN//EC
Xét tứ giác AMEB có
I là trung điểm chung của AE và MB
nên AMEB là hình bình hành
=>AM//BE
mà AN//BE
nên M,A,N thẳng hàng
1 tháng 7 2021
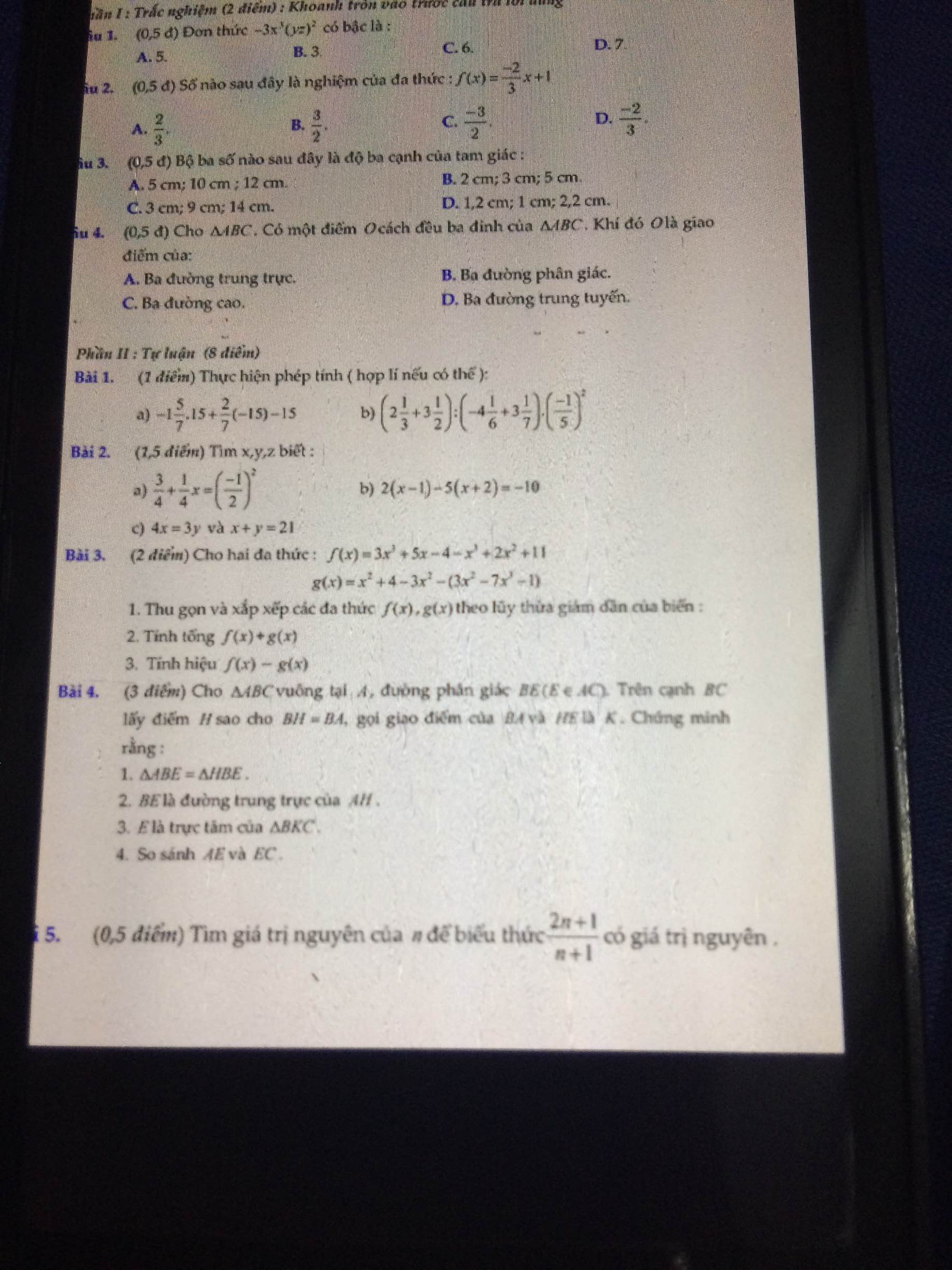
Bài 4:
a) Xét ΔABE và ΔHBE có
BA=BH(gt)
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
BE chung
Do đó: ΔABE=ΔHBE(c-g-c)
b) Ta có: ΔABE=ΔHBE(cmt)
nên EA=EH(hai cạnh tương ứng)
Ta có: BA=BH(gt)
nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: EA=EH(cmt)
nên E nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
c) Ta có: ΔABE=ΔHBE(cmt)
nên \(\widehat{BAE}=\widehat{BHE}\)(hai góc tương ứng)
mà \(\widehat{BAE}=90^0\)(gt)
nên \(\widehat{BHE}=90^0\)
Xét ΔBKC có
KH là đường cao ứng với cạnh BC
CA là đường cao ứng với cạnh BK
KH cắt CA tại E
Do đó: E là trực tâm của ΔBKC(Tính chất ba đường cao của tam giác)
d) Ta có: EA=EH(cmt)
mà EH<EC(ΔEHC vuông tại H có EC là cạnh huyền)
nên EA<EC
3T
1
18 tháng 6 2023
4:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hcn
=>ΔACD vuông tại C
b: Xét ΔKAB vuông tại A và ΔKCD vuông tại C có
KA=KC
AB=CD
=>ΔKAB=ΔKCD
=>KB=KD
c: Xét ΔACD có
DK,CM là trung tuyến
DK cắt CM tại I
=>I là trọng tâm
=>KI=1/3KD
Xét ΔCAB có
AM,BK là trung tuyến
AM cắt BK tại N
=>N là trọng tâm
=>KN=1/3KB=KI
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{b-a}{5-3}=\dfrac{-16}{2}=-8\)
Do đó: a=-24; b=-40