Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

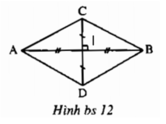
Gọi I là giao điểm của AC và BD
Ta có: I là trung điểm AC nên IA = IC = AC/2=6cm
Vì I là trung điểm của BD nên IB = ID = BD/2=8cm
Áp dụng định lí pitago vào tam giác vuông AIB ta có:
AB2=IA2+IB2
AB2=62+82=36+64=100
Vậy AB = 10 cm
Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)
Suy ra: AD = BC = CD = AB = 10cm

A C B D M
Gọi M là giao của AC và BD
Ta có: AC = 12 cm
M là trung điểm AC => AM = MC = 6 cm
Ta có: BD = 16 cm
M là trung điểm BD => BM = MD = 8 cm
Xét hai tam giác vuông ABM và CBM có:
BM: cạnh chung
AM = CM (cmt)
=> tam giác ABM = tam giác CBM (1)
Xét hai tam giác CBM và ADM có:
AM = MC (cmt)
BMC = AMD (đđ)
BM = MD (cmt)
=> tam giác CBM = tam giác ADM (2)
Xét hai tam giác vuông ADM và CDM có:
CM: chung
AM = MC (cmt)
=> tam giác ADM = tam giác CDM (3)
Từ (1);(2);(3)
=> bốn tam giác ABM; BCM; CAM; DAM bằng nhau
=> AB = BC = CD = DA
Ta có: tam giác ABM vuông
theo định lí pytago ta có:
AB2 = AM2 + BM2
=> AB2 = 62 + 82
=> AB2 = 100
=> AB = 10 cm
Có: AB = BC = CD = DA = 10 cm
Vậy: AB = 10 cm
BC = 10 cm
CD = 10 cm
DA = 10 cm.

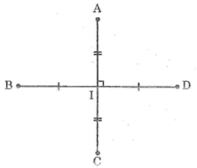
+ Gọi giao điểm của AB và CD là I. Theo giả thiết I là trung điểm của CD và AB.
+) Xét tam giác ACI và tam giác ADI có:
AI chung
CI = DI (vì I là trung điểm của CD).
∠AIC = ∠ DIA = 90º ( vì AB vuông góc với CD tại I).
Suy ra: ∆ ACI = ∆ ADI (c.g.c)
Suy ra: ∠CAI = ∠ ADI ( hai góc tương ứng).
Do đó, AB là tia phân giác của góc ∠CAD .
+) Chứng minh tương tự ta có: CD là tia phân giác của góc C, BA là tia phân giác của góc B, DC là tia phân giác của góc D.

a Đặt tên điểm nằm giữa là I nhé. Vì 2 đoạn thẳng AB và CD cắt nhau tại trung điểm nên suy ra 2 cạnh IC=ID Sau đó xét tam giác bằng nhau trường hợp cạnh-góc-cạnh và suy ra các đoạn thảng bằng nhau b Vì AB và CD vuông góc suy ra góc AID = 90 độ, xong tính các góc kia cũng ra 90 độ bằng cách 2 góc kề bù rồi chia 2 là ra tia p/g



giups mik nha