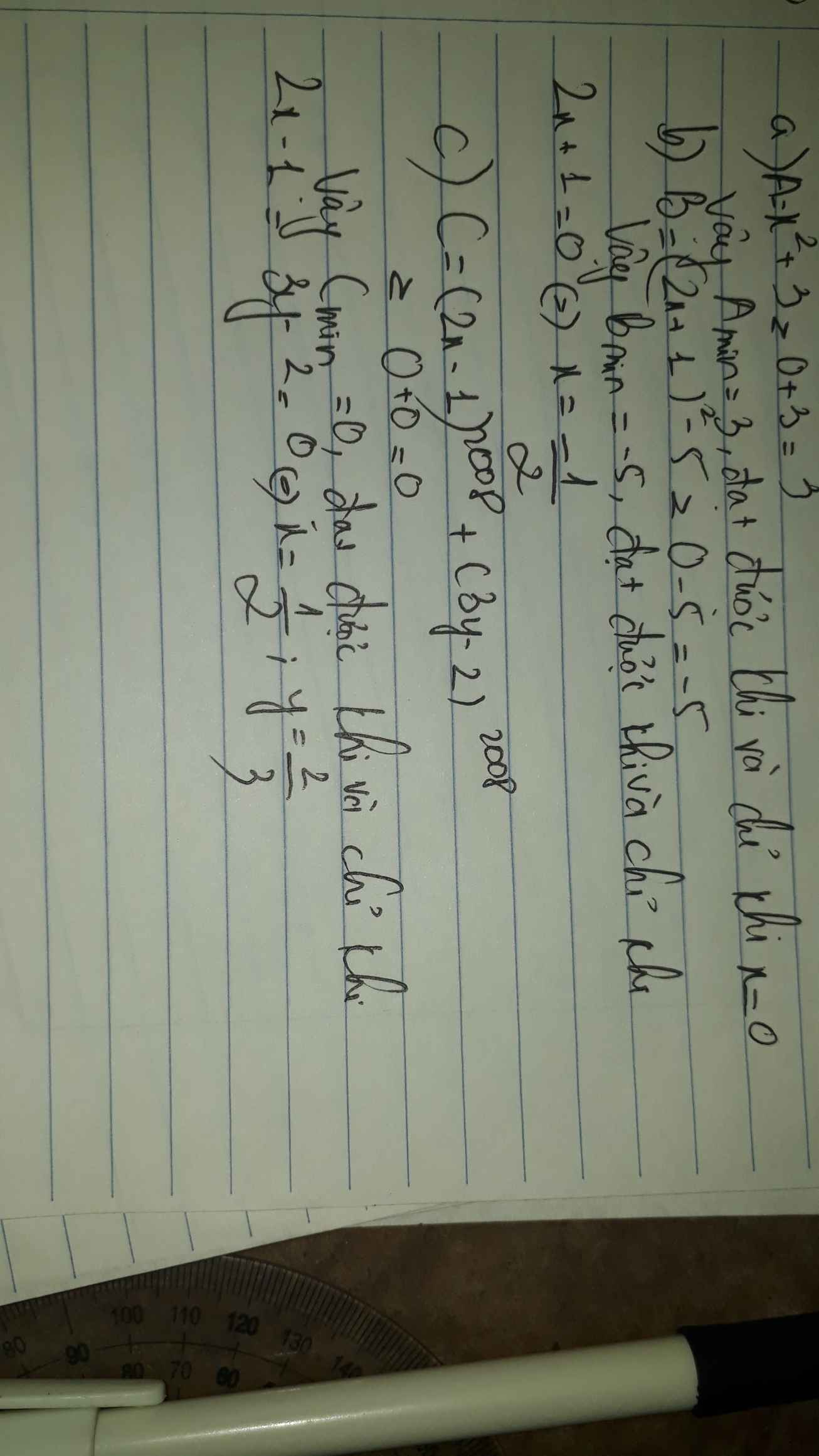NH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 8 2021
a)Ta có: \(x^2\ge0\Rightarrow x^2+3\ge3\)
Dấu "=" xảy ra \(\Leftrightarrow x=0\)
Vậy \(A_{Min}=3 khi x=0\)
b) \(\left(2x+1\right)^2\ge0\Rightarrow\left(2x+1\right)^2-5\ge-5\)
Dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(B_{Min}=-5khix=-\dfrac{1}{2}\)
c) \(\left(2x-1\right)^{2008}\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{1}{2}\)
\(\left(3y-2\right)^{2008}\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow y=\dfrac{2}{3}\)
\(\Rightarrow\left(2x-1\right)^{2008}+\left(3y-2\right)^{2008}\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{2}{3}\end{matrix}\right.\)
Vậy \(C_{Min}=0khix=\dfrac{1}{2}vày=\dfrac{2}{3}\)
CW
28 tháng 10 2016
x=2009 => 2008 = x-1
Thay x=2009 và 2008 = x -1 vào A:
\(A=x^{2009}-\left(x-1\right)\cdot x^{2008}-\left(x-1\right)\cdot x^{2007}-...-\left(x-1\right)\cdot x+1\)
\(=x^{2009}-x^{2009}+x^{2008}-x^{2008}+.....-x^2+x+1\)
\(=x+1=2009+1=2010\)
11 tháng 11 2016
Ta có
\(\frac{a_1}{a_2}+\frac{a_2}{a_3}+...+\frac{a_{2008}}{a_1}=\frac{a_1+...+a_{12}+...+a_{2008}}{a_2+a_3+...+a_1}=1\)
Từ đó a1 = a2 = a3 = ... = a2008
\(\Rightarrow N=\frac{a^2_1+a^2_2+...+a_{2008}^2}{\left(a_1+a_2+...+a_{2008}\right)^2}=\frac{2008a^2_1}{\left(2008a_1\right)^2}=\frac{1}{2008}\)
29 tháng 11 2016
Ta thấy : \(\left(2x-1\right)^{2008}\ge0\)
\(\left(y-\frac{2}{5}\right)^{2008}\ge0\)
\(\left|x+y+z\right|\ge0\)
Để \(\left(2x-1\right)^{2008}+\left(y-\frac{2}{5}\right)^{2008}+\left|x+y+z\right|=0\)
\(\Leftrightarrow\hept{\begin{cases}2x-1=0\\y-\frac{2}{5}=0\\x+y=z=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{2}{5}\\z=-x-y\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{2}{5}\\z=\frac{-1}{2}-\frac{2}{5}\end{cases}}\)
NT
0
HT
2