Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)

a)\(-1\le sinx\le1\)
\(\Leftrightarrow1\ge-sinx\ge-1\)
\(\Leftrightarrow4\ge3-sinx\ge2\) \(\Leftrightarrow16\ge\left(3-sinx\right)^2\ge4\)\(\Leftrightarrow17\ge\left(3-sinx\right)^2+1\ge5\)
\(\Leftrightarrow17\ge y\ge5\)
\(y_{min}=5\Leftrightarrow sinx=1\)\(\Leftrightarrow\)\(x=\dfrac{\pi}{2}+k2\pi\)\(\left(k\in Z\right)\)
\(y_{max}=17\Leftrightarrow\)\(sinx=-1\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\)\(\left(k\in Z\right)\)
b)\(y=\left(sin^2x+cos^2x\right)^2-2.sinx^2cos^2x\)\(=1-\dfrac{1}{2}.sin^22x\)
Có \(0\le sin^22x\le1\)\(\Leftrightarrow0\ge-\dfrac{1}{2}.sin^22x\ge-\dfrac{1}{2}\)
\(\Leftrightarrow1\ge1-\dfrac{1}{2}.sin^22x\ge\dfrac{1}{2}\)\(\Leftrightarrow1\ge y\ge\dfrac{1}{2}\)
\(y_{min}=\dfrac{1}{2}\Leftrightarrow sin^22x=1\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}sin2x=-1\\sin2x=1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
\(y_{max}=1\Leftrightarrow sin2x=0\Leftrightarrow x=\dfrac{k\pi}{2}\)\(\left(k\in Z\right)\)
c)\(y=\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=1-3sin^2x.cos^2x=1-\dfrac{3}{4}.sin^22x\)
Có \(0\le sin^22x\le1\)\(\Leftrightarrow0\ge-\dfrac{3}{4}.sin^22x\ge-\dfrac{3}{4}\)
\(\Leftrightarrow1\ge1-\dfrac{3}{4}.sin^22x\ge\dfrac{1}{4}\)\(\Leftrightarrow1\ge y\ge\dfrac{1}{4}\)
\(y_{min}=\dfrac{1}{4}\Leftrightarrow sin^22x=1\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(y_{max}=1\Leftrightarrow sin2x=0\Leftrightarrow x=\dfrac{k\pi}{2}\)\(\left(k\in Z\right)\)
Vậy...
a, Đặt \(t=sinx\left(t\in\left[-1;1\right]\right)\)
\(y=f\left(t\right)=\left(3-t\right)^2+1=t^2-6t+10\)
\(\Rightarrow min=min\left\{f\left(-1\right);f\left(1\right)\right\}=f\left(1\right)=5\)
\(\Rightarrow max=max\left\{f\left(-1\right);f\left(1\right)\right\}=f\left(-1\right)=17\)
b, \(y=sin^4x+cos^4x=1-2sin^2x.cos^2x=1-\dfrac{1}{2}sin^22x\)
Đặt \(t=sin2x\left(t\in\left[-1;1\right]\right)\)
\(y=f\left(t\right)=1-\dfrac{1}{2}t^2\)
\(\Rightarrow min=min\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=\dfrac{1}{2}\)
\(\Rightarrow max=max\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=1\)
c, \(y=sin^6x+cos^6x\)
\(=sin^4x+cos^4x-sin^2x.cos^2x\)
\(=1-3sin^2x.cos^2x\)
\(=1-\dfrac{3}{4}sin^22x\)
Đặt \(t=sin2x\left(t\in\left[-1;1\right]\right)\)
\(y=f\left(t\right)=1-\dfrac{3}{4}t^2\)
\(\Rightarrow min=min\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=\dfrac{1}{4}\)
\(\Rightarrow max=max\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=1\)


a: -1<=sin x<=1
=>-1+3<=sin x+3<=1+3
=>2<=sinx+3<=4
=>\(\dfrac{1}{2}>=\dfrac{1}{sinx+3}>=\dfrac{1}{4}\)
=>\(2>=\dfrac{4}{sinx+3}>=1\)
=>\(-2< =-\dfrac{4}{sinx+3}< =-1\)
=>-2+3<=y<=-1+3
=>1<=y<=2
y=1 khi \(\dfrac{-4}{sinx+3}+3=1\)
=>\(\dfrac{-4}{sinx+3}=-2\)
=>sinx+3=2
=>sin x=-1
=>x=-pi/2+k2pi
y=3 khi sin x=1
=>x=pi/2+k2pi
b: -1<=cosx<=1
=>4>=-4cosx>=-4
=>9>=-4cosx+5>=1
=>2/9<=2/5-4cosx<=2
=>2/9<=y<=2
\(y_{min}=\dfrac{2}{9}\) khi \(\dfrac{2}{5-4cosx}=\dfrac{2}{9}\)
=>\(5-4\cdot cosx=9\)
=>4*cosx=4
=>cosx=1
=>x=k2pi
y max khi cosx=-1
=>x=pi+k2pi
c: \(0< =cos^2x< =1\)
=>\(0< =2\cdot cos^2x< =2\)
=>\(-1< =y< =2\)
y min=-1 khi cos^2x=0
=>x=pi/2+kpi
y max=2 khi cos^2x=1
=>sin^2x=0
=>x=kpi



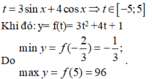
1) a) y = 3sinx - 1
Ta có: -1 ≤ sinx ≤ 1
<=> -3 ≤ 3sinx ≤ 3
<=> -4 ≤ 3sinx - 1 ≤ 2
Vậy GTLN of HS là 2 đạt đc khi sinx = 1 <=> x = π/2 + k2π
GTNN of HS là -4 đạt đc khi sinx = -1 <=> x = -π/2 + k2π
b) y = cos^2(2x) - 3
Ta có: 0 ≤ cos^2(2x) ≤ 1
<=> -3 ≤ cos^2(2x) - 3 ≤ -2
Vậy GTLN of HS là -2 đạt đc khi cos^2(2x) = 1
<=> x = kπ
GTNN of HS là -3 đạt đc khi cos^2(2x) = 0
<=> x = π/4 + kπ/2
c) y = 3sin2x - 5
Ta có: -1 ≤ sin2x ≤ 1
<=> -3 ≤ 3sin2x ≤ 3
<=> -8 ≤ 3sin2x - 5 ≤ -2
Vậy GTLN of HS là -2 đạt đc khi sin2x = 1 <=> x = π/4 + kπ
GTNN of HS là -8 đạt đc khi sin2x = -1 <=> x = -π/4 + kπ
d) y = [căn(sinx + 3)] - 1
Ta có: 0 ≤ căn(sinx) ≤ 1
<=> căn 3 ≤ căn(sinx + 3) ≤ 1+ căn 3
<=> -1 + căn 3 ≤ [căn(sinx + 3)] - 1 ≤ căn 3
Vậy GTLN of HS là căn 3 đạt đc khi sinx = 1 <=> x = π/2 + k2π
GTNN of HS là -1 + căn 3 đạt đc khi sinx = 0 <=> x = kπ