Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Xét tứ giác MNPQ có
G là trung điểm của đường chéo MP(gt)
G là trung điểm của đường chéo NQ(gt)
Do đó: MNPQ là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b)
Xét ΔABC có
BM là đường trung tuyến ứng với cạnh AC(gt)
CN là đường trung tuyến ứng với cạnh AB(gt)
BM cắt CN tại G(gt)
Do đó: G là trọng tâm của ΔABC(Định lí ba đường trung tuyến của tam giác)
Suy ra: \(MG=\dfrac{1}{3}MB;BG=\dfrac{2}{3}MB;NG=\dfrac{1}{3}NC;CG=\dfrac{2}{3}NC\)(1)
Ta có: G là trung điểm của MP(gt)
nên MG=GP
mà \(MG=\dfrac{1}{3}MB\)
nên \(MG=GP=\dfrac{1}{3}MB\)
Ta có: MG+GP=MP(G nằm giữa M và P)
nên \(MP=\dfrac{1}{3}MB+\dfrac{1}{3}MB=\dfrac{2}{3}MB\)(1)
Ta có: G là trung điểm của NQ(gt)
nên \(GN=GQ=\dfrac{1}{3}NC\)
Ta có: NG+GQ=NQ(G là trung điểm của NQ)
nên \(NQ=\dfrac{1}{3}NC+\dfrac{1}{3}NC=\dfrac{2}{3}NC\)(2)
Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔBAC cân tại A)
nên AN=NB=AM=MC
Xét ΔAMB và ΔANC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAM}\) chung
AM=AN(cmt)
Do đó: ΔAMB=ΔANC(c-g-c)
Suy ra: BM=CN(hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra NQ=MP
Hình bình hành MNPQ có NQ=MP(cmt)
nên MNPQ là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

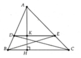
a: Ta có: D đối xứng với A qua BC
nên BC là đường trung trực của AD
=>BC vuông góc với AD tại trung điểm của AD
=>F là trung điểm của AD
Ta có: ΔABC cân tại A
mà AF là đường cao
nên F là trung điểm của BC
Xét tứ giác ABDC có
F là trung điểm của AD
F là trung điểm của BC
Do đó:ABDC là hình bình hành
mà AB=AC
nên ABDC là hình thoi
b: Xét ΔEBC có
BA là đường trung tuyến
BA=EC/2
Do đó:ΔEBC vuông tại B
=>EB\(\perp\)BC
c: Xét tứ giác ADBE có
AD//BE
AD=BE
Do đó; ADBE là hình bình hành
Trả lời:
A B C N M P G
a, Xét tam giác ABC có:
AM là đường trung tuyến thứ nhất
BN là đường trung tuyến thứ hai
Mà AM và BN cắt nhau tại G (gt)
=> G là trọng tâm của tam giác ABC
=> CG là đường trung tuyến thứ 3
hay CP là đường trung tuyến thứ 3 ( ứng với cạnh AB )
=> P là trung điểm của AB (đpcm)
b, Xét tam giác ABC có:
P là trung điểm của AB (cmt)
N là trung điểm của AC (gt)
=> PN là đường trung bình của tam giác ABC
=> PN // BC
Vì tam giác ABC cân tại A (gt)
=> ^ABC = ^ACB
Xét tứ giác BPNC có:
PN // BC (cmt)
=> tứ giác BPNC là hình thang
Mà ^ABC = ^ACB (cmt)
=> BPNC là hình thang cân
c, Xét tam giác ABC có:
P là trung điểm của AB (cmt)
M là trung điểm của BC (gt)
=> PM là đường trung bình của tam giác ABC
=> PM // AC
Xét tứ giác APMC có:
PM // AC (cmt)
^PAC \(\ne\)^ACM
=> tứ giác APMC là hình thang