TB
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QL
1
17 tháng 6 2018
ĐKXĐ: \(x\ge2\)
\(A=\sqrt{2}-\sqrt{x+2\sqrt{2x-4}}\)
\(=\sqrt{2}-\sqrt{x-2+2\sqrt{x-2}.\sqrt{2}+2}\)
\(=\sqrt{2}-\sqrt{\left(\sqrt{x-2}+\sqrt{2}\right)^2}\)
\(=\sqrt{2}-\left(\sqrt{x-2}+\sqrt{2}\right)=-\sqrt{x-2}\)
\(A=-1\) \(\Leftrightarrow\) \(-\sqrt{x-2}=-1\)
\(\Leftrightarrow\) \(x-2=1\)
\(\Leftrightarrow\) \(x=3\) (t/m ĐKXĐ)
Vậy...
I
1
30 tháng 6 2019
\(A=\sqrt{2}-\sqrt{\left(\sqrt{2}+\sqrt{x-2}\right)^2}\)
\(=\sqrt{2}-\left(\sqrt{2}+\sqrt{x-2}\right)=-\sqrt{x-2}\)
Để A=-1 thì \(-\sqrt{x-2}=-1\Leftrightarrow\sqrt{x-2}=1\)
\(\Leftrightarrow x-2=1\Rightarrow x=3\)
23 tháng 10 2021
a: TXĐ: D=[0;+\(\infty\))\{1}
\(B=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}-\dfrac{\sqrt{x}}{x-1}\)
\(=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\cdot2}\)
\(=\dfrac{-1}{\sqrt{x}+1}\)
23 tháng 10 2021
\(a,ĐK:x\ge0\\ x\ne1\\ B=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ B=\dfrac{2\left(1-\sqrt{x}\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\\ b,x=3\Leftrightarrow B=\dfrac{-1}{\sqrt{3}+1}=\dfrac{1-\sqrt{3}}{2}\\ c,\left|B\right|=\dfrac{1}{2}\Leftrightarrow\left|\dfrac{-1}{\sqrt{x}+1}\right|=\dfrac{1}{2}\\ \Leftrightarrow\dfrac{1}{\sqrt{x}+1}=\dfrac{1}{2}\left(\sqrt{x}+1\ge1>0\right)\\ \Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)
28 tháng 5 2021
ĐKXĐ: \(x\ge0;x\ne1\)
Ta có: \(A=\left(2+\dfrac{2x+\sqrt{x}}{2\sqrt{x}+1}\right)\left(2-\dfrac{x-\sqrt{x}}{\sqrt{x}-1}\right)\)
\(A=\left(2+\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{2\sqrt{x}+1}\right)\left(2-\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\right)\)
\(A=\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)=4-x\)
25 tháng 8 2021
Ta có: \(A=\left(\dfrac{\sqrt{x}+1}{x+1}-\dfrac{4-3\sqrt{x}}{x-4\sqrt{x}+4}\right):\left(\dfrac{x-\sqrt{x}}{x\sqrt{x}-2x+\sqrt{x}-2}\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-4\sqrt{x}+4\right)+\left(3\sqrt{x}-4\right)\left(x+1\right)}{\left(x+1\right)\left(\sqrt{x}-2\right)^2}:\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-2\right)\left(x+1\right)}\)
\(=\dfrac{x\sqrt{x}-4x+4\sqrt{x}+x-4\sqrt{x}+4+3x\sqrt{x}+3\sqrt{x}-4x-4}{\left(x+1\right)\left(\sqrt{x}-2\right)^2}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(x+1\right)}{x-\sqrt{x}}\)
\(=\dfrac{4x\sqrt{x}-7x+3\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\cdot\left(4\sqrt{x}-3\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4\sqrt{x}-3}{\sqrt{x}-2}\)
Để A>1 thì A-1>0
\(\Leftrightarrow\dfrac{4\sqrt{x}-3-\sqrt{x}+2}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\dfrac{3\sqrt{x}-1}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}3\sqrt{x}-1\le0\\\sqrt{x}-2>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}0< x\le\dfrac{1}{9}\\x>4\end{matrix}\right.\)
8 tháng 10 2017
1.
a. ĐKXĐ : x lớn hơn hoặc bằng 1/2
b. A\(\sqrt{2}\)= \(\sqrt{2x+2\sqrt{2x-1}}-\sqrt{2x-2\sqrt{2x-1}}\)
= \(\sqrt{2x-1+1+2\sqrt{2x-1}}-\sqrt{2x-1+1-2\sqrt{2x-1}}\)
=\(\sqrt{\left(\sqrt{2x-1}+1\right)^2}-\sqrt{\left(\sqrt{2x-1}-1\right)^2}\)
= \(\sqrt{2x-1}+1-\left|\sqrt{2x-1}-1\right|\)
Nếu \(x\ge1thìA\sqrt{2}=\sqrt{2x-1}+1-\left(\sqrt{2x-1}-1\right)=2\)
\(\Rightarrow A=2\)
Nếu 1/2 \(\le x< 1thìA\sqrt{2}=\sqrt{2x-1}+1-\left(1-\sqrt{2x-1}\right)=2\sqrt{2x-1}\)
Do đó : A= \(\sqrt{4x-2}\)
Vậy ............
8 tháng 10 2017
2.
a. \(x\ge2\)hoặc x<0
b. A= \(2\sqrt{x^2-2x}\)
c. A<2 \(\Leftrightarrow\)\(2\sqrt{x^2-2x}< 2\Leftrightarrow\sqrt{x^2-2x}< 1\Leftrightarrow x^2-2x< 1\Leftrightarrow\left(x-1\right)^2< 2\)
\(-\sqrt{2}< x-1< \sqrt{2}\Leftrightarrow1-\sqrt{2}< x< 1+\sqrt{2}\)
Kết hợp vs đk câu a , ta đc : \(1-\sqrt{2}< x< 0và2\le x< 1+\sqrt{2}\)
Vậy...........
31 tháng 10 2021
\(1,\\ a,ĐK:\left\{{}\begin{matrix}x\ge0\\x+5\ge0\end{matrix}\right.\Leftrightarrow x\ge0\\ b,Sửa:B=\left(\sqrt{3}-1\right)^2+\dfrac{24-2\sqrt{3}}{\sqrt{2}-1}\\ B=4-2\sqrt{3}+\dfrac{2\sqrt{3}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}\\ B=4-2\sqrt{3}+2\sqrt{3}=4\\ 3,\\ =\left[1-\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{1+\sqrt{x}}\right]\cdot\dfrac{\sqrt{x}-3+2-2\sqrt{x}}{\left(1-\sqrt{x}\right)\left(\sqrt{x}-3\right)}-2\\ =\left(1-\sqrt{x}\right)\cdot\dfrac{-\sqrt{x}-1}{\left(1-\sqrt{x}\right)\left(\sqrt{x}-3\right)}-2\\ =\dfrac{-\sqrt{x}-1}{\sqrt{x}-3}-2=\dfrac{-\sqrt{x}-1-2\sqrt{x}+6}{\sqrt{x}-3}=\dfrac{-3\sqrt{x}+5}{\sqrt{x}-3}\)
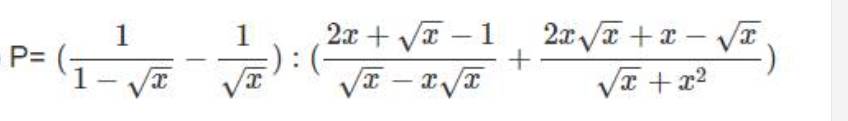
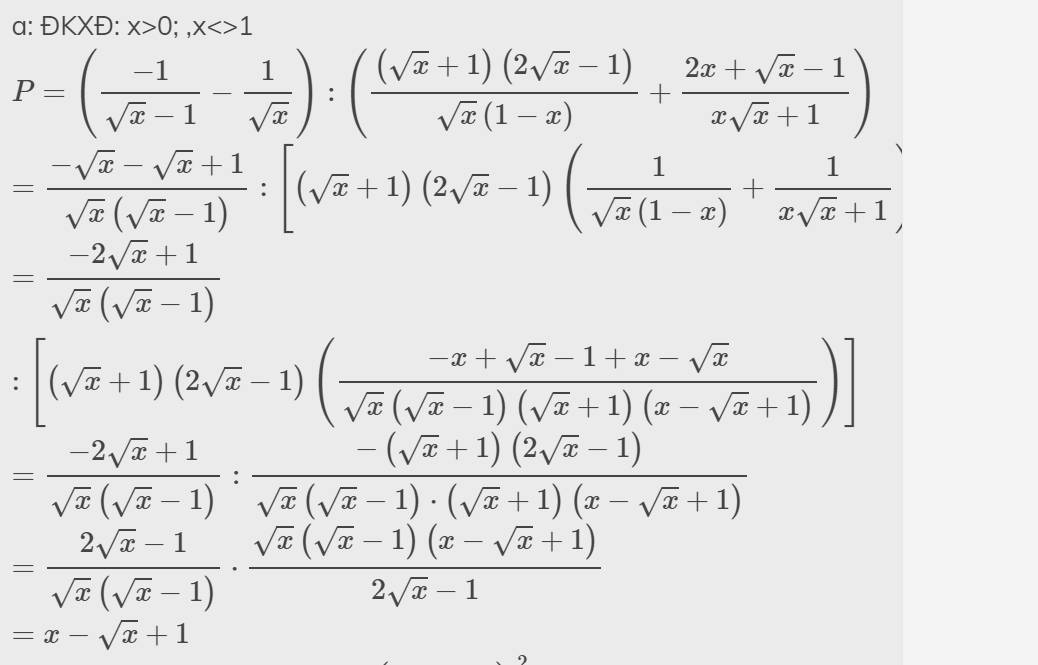
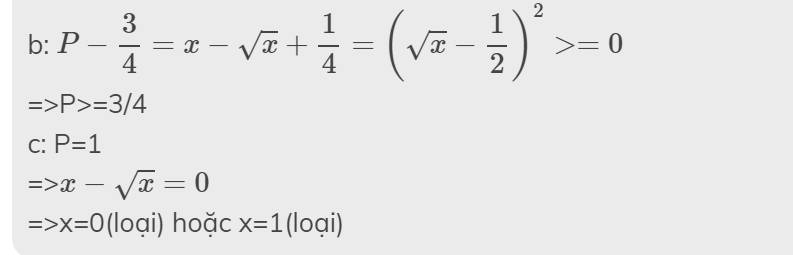
ĐKXĐ:
\(2x-4\ge0\text{ và }x+2\sqrt{2x-4}\ge0\)
<=>\(2x\ge4\text{ và }x\ge2\sqrt{2x-4}\)
<=>\(x\ge2\text{ và }x^2\ge8x-16\)
<=>\(x\ge2\text{ và }\left(x-4\right)^2\ge0\)
<=>\(x\ge2\)
\(A=\sqrt{2}-\sqrt{x+2\sqrt{2x-4}}=\sqrt{2}-\sqrt{x+2\sqrt{2}\sqrt{x-2}}\)
\(=\sqrt{2}-\sqrt{2+2\sqrt{2}\sqrt{x-2}+x-2}=\sqrt{2}-\sqrt{\left(\sqrt{2}-\sqrt{x-2}\right)^2}\)
\(=\sqrt{2}-\left|\sqrt{2}-\sqrt{x-2}\right|\)
Với \(\sqrt{x-2}\ge\sqrt{2}\text{ thì }A=\sqrt{2}-\sqrt{x-2}+\sqrt{2}=2\sqrt{2}-\sqrt{x-2}\)
Với \(\sqrt{x-2}\le\sqrt{2}\text{ thì }A=\sqrt{2}-\sqrt{2}+\sqrt{x-2}=\sqrt{x-2}\)
TH1: \(\sqrt{x-2}\ge\sqrt{2}\)
Để A=-1 thì
\(2\sqrt{2}-\sqrt{x-2}=-1\)
<=>\(\sqrt{x-2}=2\sqrt{2}-1\)
<=>\(x-2=9-4\sqrt{2}\)
<=>\(x=11-4\sqrt{2}\)(TM)
TH2: \(\sqrt{x-2}\le\sqrt{2}\)
Để A=-1 thì :
\(\sqrt{x-2}=-1\)(Vô lí)
Vậy \(x=11-4\sqrt{2}\)