Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B 50km 2h 30p x km/h x+2 km/h
Đổi \(30p=\frac{1}{2}h\)
Gọi vận tốc dự định của người đó là x (km/h) (x > 0)
\(\Rightarrow\) thời gian dự định của người đó là : \(t_{dđ}=\frac{S_{AB}}{v_{dđ}}=\frac{50}{x}\) (h)
Quãng đường ng đó di chuyển được sau 2 giờ là : \(2x\) (km)
\(\Rightarrow\)Quãng đường còn lại là \(50-2x\) (km)
Người đó phải tăng vận tốc thêm 2km/h trên quãng đường còn lại để đến B đúng dự định nên ta có PT :
\(\frac{50}{x}=2+\frac{1}{2}+\frac{50-2x}{x+2}\)
\(\Leftrightarrow\frac{50}{x}=\frac{5}{2}+\frac{50-2x}{x+2}\)
\(\Leftrightarrow\frac{50}{x}=\frac{5x+10+100-4x}{2\left(x+2\right)}\Leftrightarrow\frac{50}{x}=\frac{x+110}{2x+4}\)
\(\Leftrightarrow x^2+110x-100x-200=0\)
\(\Leftrightarrow x^2+10x-200=0\)
\(\Leftrightarrow\left(x-10\right)\left(x+20\right)\Rightarrow\orbr{\begin{cases}x=10\\x=-20\left(l\right)\end{cases}}\)
Vậy vận tốc ban đầu của xe là 10 km/h
Quãng đường AB dài là:
60 x 2 = 120 (km)
Nếu người đó đi với vận tốc 40km/h thì cần thời gian là:
120: 40 = 3 giờ

GỌI VẬN TỐC BAN ĐẦU LÀ V ,THỜI GIAN DỰ ĐỊNH LÀ T, THỜI GIAN ĐI QUANG ĐƯỜNG CON LẠI LÀ T' (ĐK V,T,T'>0)
S=V*T=V*2+(V+2)*T'
\(\Rightarrow V\cdot T=2V+\left(V+2\right)\cdot T'\)
TA LẠI CÓ :T'=T-2-0,5
\(\Rightarrow V\cdot T=2V+\left(V+2\right)\cdot\left(T-2-0,5\right)\)
\(\Rightarrow2T-5=0,5\cdot V\Rightarrow T=\frac{\left(0,5\cdot V+5\right)}{2}\)
MÀ V*T=50\(\Rightarrow V\cdot\frac{\left(0,5V+5\right)}{2}=50\Rightarrow V=10;-20\)
VÌ V>0 V=10...

gọi v là vận tốc bđ
thời gian dự đinh là 50/y
qđ còn lại sau khi đi dk 2h là 50-2v
thời gian đi qđ còn lại là 50-2v/(v+2)
từ giả thiết đề bài cho ta có pt
50-2v/(v+2)+2+30/60=50/v
bạn tự giải pt nha mk hướng dẫn tek thui

Gọi vận tốc dự định là x
Vận tốc đi trên S còn lại là : x+10 Dk :x>0
Vì người đó đến B sớm hơn dự định 24phut (=0,4h) nên ta có pt :
40/x +80/x+10 +0,4 = 120/x
0,4 = 80/x - 80/x+10
0,4=800/x(x+10)
x2+10x=2000
x2+10x-2000=0
(x-40)(x+50)=0
Vi x>0 => x+50>0
=> x-40 =0
x=40(km/h)

Đáp án A
Gọi vận tốc ban đầu của người đó là x (km/h) (x > 0).
Thời giạn dự định người đó đi hết quãng đường là 90/x (h).
Quãng đường người đó đi được sau 1 giờ là x (km).
Quãng đường còn lại người đó phải tăng tốc là 90 – x (km).
Vận tốc của người đó sau khi tăng tốc là x + 4 (km/h).
Thời gian người đó đi hết quãng đường còn lại là 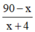 (h).
(h).
Theo đề bài ta có phương trình:
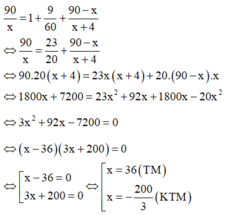
Vậy vận tốc lúc đầu của người đó là 36 km/h.
cho mk sửa: D thuộc HC và E là hình chiếu của C thuộc AD