Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 3x^2-4x+1=0
a=3; b=-4; c=1
Vì a+b+c=0 nên phương trình có hai nghiệm là:
x1=1 và x2=c/a=1/3
b: -x^2+6x-5=0
=>x^2-6x+5=0
a=1; b=-6; c=5
Vì a+b+c=0 nên phương trình có hai nghiệm là;
x1=1; x2=5/1=5

\(1,\Delta=\left(-11\right)^2-4\cdot30=1\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11-1}{2}=5\\x=\dfrac{11+1}{2}=6\end{matrix}\right.\\ 2,\Delta=\left(-1\right)^2-4\left(-20\right)=81\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{81}}{2}=-4\\x=\dfrac{1+\sqrt{81}}{2}=5\end{matrix}\right.\\ 3,\Delta=14^2-4\cdot24=100\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-14-\sqrt{100}}{2}=-12\\x=\dfrac{-14+\sqrt{100}}{2}=-2\end{matrix}\right.\\ 4,\Delta=8^2-4\left(-2\right)3=88\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-8-\sqrt{88}}{6}=\dfrac{-4+\sqrt{22}}{3}\\x=\dfrac{-8+\sqrt{88}}{6}=\dfrac{-4-\sqrt{22}}{3}\end{matrix}\right.\)

a) Phương trình bậc hai 4 x 2 + 4 x + 1 = 0
Có a = 4; b’ = 2; c = 1; Δ ’ = ( b ’ ) 2 – a c = 2 2 – 4 . 1 = 0
Phương trình có nghiệm kép là:
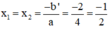
b) Phương trình 13852 x 2 – 14 x + 1 = 0
Có a = 13852; b’ = -7; c = 1;
Δ ’ = ( b ’ ) 2 – a c = ( - 7 ) 2 – 13852 . 1 = - 13803 < 0
Vậy phương trình vô nghiệm.
c) Phương trình bậc hai 5 x 2 – 6 x + 1 = 0
Có: a = 5; b’ = -3; c = 1.; Δ ’ = ( b ’ ) 2 – a c = ( - 3 ) 2 – 5 . 1 = 4 > 0
Phương trình có hai nghiệm phân biệt:
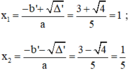
d) Phương trình bậc hai: ![]()
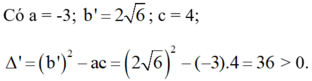
Phương trình có hai nghiệm phân biệt :
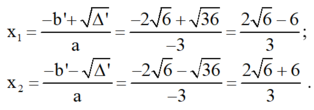
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 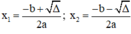
+ Nếu Δ = 0, phương trình có nghiệm kép 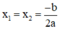 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.

d, \(\Delta'=225-25.9=0\)pt có nghiệm kép
\(x_1=x_2=\dfrac{-15}{9}=-\dfrac{5}{3}\)
e, \(\Delta'=4.5-4=16>0\)pt có 2 nghiệm pb
\(x_1=2\sqrt{5}-4;x_2=2\sqrt{5}+4\)
d: \(\Leftrightarrow\left(3x+5\right)^2=0\)
=>3x+5=0
hay x=-5/3
e: \(\text{Δ}=\left(4\sqrt{5}\right)^2-4\cdot1\cdot4=80-16=64>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{4\sqrt{5}-8}{2}=2\sqrt{5}-4\\x_2=2\sqrt{5}+4\end{matrix}\right.\)

Phương trình 5 x 2 – 6x -1 = 0 có hệ số a = 5, b’ = -3, c = -1
Ta có: ∆ ’ = b ' 2 – ac = - 3 2 -5.(-1) = 9 + 5 = 14 > 0
∆ ' = 14
Phương trình có hai nghiệm phân biệt :
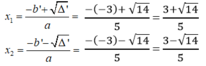

a) 5 x 2 – x + 2 = 0 ;
a = 5; b = -1; c = 2
Δ = b 2 - 4 a c = ( - 1 ) 2 - 4 . 5 . 2
= 1 - 40 = -39 < 0
Vậy phương trình trên vô nghiệm.
b) 4 x 2 – 4 x + 1 = 0 ;
a = 4; b = -4; c = 1
Δ = b 2 - 4 a c = ( - 4 ) 2 - 4 . 4 . 1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
c) - 3 x 2 + x + 5 = 0
a = -3; b = 1; c = 5
Δ = b 2 - 4 a c = 12 - 4 . ( - 3 ) . 5 = 1 + 60 = 61 > 0
⇒ Do Δ >0 nên áp dụng công thức nghiệm, phương trình có 2 nghiệm phân biệt
x 1 = ( 1 - √ 61 ) / 6 ; x 2 = ( 1 + √ 61 ) / 6

Phương trình 9 x 2 +6x+1 =0 có hệ số a=9,b’=3,c=1
Ta có: ∆ ’ = b ' 2 – ac = 3 2 -9.1 = 9 - 9 = 0
Phương trình có nghiệm kép:
x 1 = x 2 = -b'/a =-3/9 =-1/3

Phương trình bậc hai 5x2 – 6x + 1 = 0
Có: a = 5; b’ = -3; c = 1.; Δ’ = (b’)2 – ac = (-3)2 – 5.1 = 4 > 0
Phương trình có hai nghiệm phân biệt:
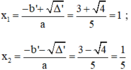

Phương trình bậc hai 4x2 + 4x + 1 = 0
Có a = 4; b’ = 2; c = 1; Δ’ = (b’)2 – ac = 22 – 4.1 = 0
Phương trình có nghiệm kép là:
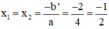
BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn).
1) x2 - 11x + 38 = 0 ;
2) 6x2 + 71x + 175 = 0 ;
3) 5x2 - 6x + 27 =0 ;
4) - 30x2 + 30x - 7,5 = 0 ;
5) 4x2 - 16x + 17 = 0 ;
6) x2 + 4x - 12 = 0 ;
Được chưa bạn?