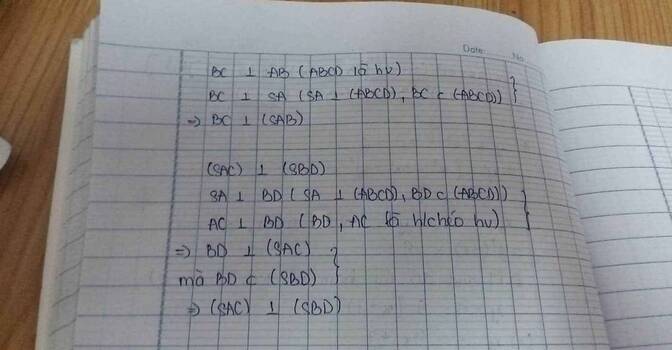Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC vuông góc SA
BC vuông góc AB
=>BC vuông góc (SAB)
=>(SAB) vuông góc (SBC)
b: BA vuông AD
BA vuông góc SA
=>BA vuông góc (SAD)
=>BA vuông góc SD
Lấy H là trung điểm của SD
=>HM//DC
=>HM vuông góc BC
ΔSAD vuông tại A nên AH vuông góc SD
=>SD vuông góc (BAH)
=>SD vuông góc (ABM)
=>(SCD) vuông góc (ABM)

a. Ta có : \(BC\perp SA;BC\perp AB\Rightarrow BC\perp\left(SAB\right)\Rightarrow\left(SAB\right)\perp\left(SBC\right)\)
b.Dễ dàng c/m : \(AB\perp\left(SAD\right)\) \(\Rightarrow AB\perp SD\)
Lấy H là TĐ SD \(\Rightarrow MH\) // DC // AB
\(\Delta SAD\) vuông cân tại A ; H là TĐ SD \(\Rightarrow AH\perp SD\)
Suy ra : \(SD\perp\left(ABH\right)\Rightarrow SD\perp\left(ABM\right)\Rightarrow\left(SCD\right)\perp\left(ABM\right)\left(đpcm\right)\)

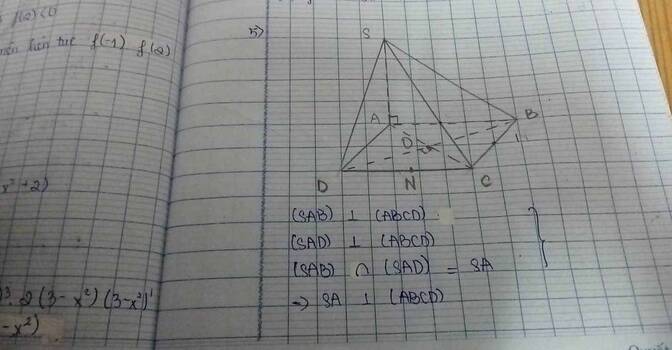
a) (SAB) và (SAD) cùng vuông góc (ABCD), (SAB) và (SAB) có giao tuyến SA => SA vuông góc (ABCD)
=> BC vuông góc SA. Mà BC vuông góc AB nên BC vuông góc (SAB).
Ta cũng có BD vuông góc AS, BD vuông góc AC vì ABCD là hình vuông
=> BD vuông góc (SAC) hay (SAC) vuông góc (SBD).
b) Gọi M là trung điểm của AB, CM cắt AD tại P, H thuộc CM sao cho AH vuông góc CM, K thuộc SH sao cho AK vuông góc SH.
Dễ thấy AN || CM => AN || (SCM) => d(AN,SC) = d(AN,SCM) = d(A,SCM) = d(A,SMP)
Ta có AH vuông góc MP, MP vuông góc AS => MP vuông góc (HAS) => (SMP) vuông góc (HAS)
Vì (SMP) và (HAS) có giao tuyến SH, AK vuông góc SH tại K nên d(A,SMP) = AK
Theo hệ thức lượng thì: \(\frac{1}{AK^2}=\frac{1}{AS^2}+\frac{1}{AM^2}+\frac{1}{AP^2}\)
\(\Rightarrow d\left(AN,SC\right)=d\left(A,SMP\right)=AK=\frac{AS.AM.AP}{\sqrt{AS^2AM^2+AM^2AP^2+AP^2AS^2}}\)
\(=\frac{a\sqrt{2}.\frac{a}{2}.a}{\sqrt{2a^2.\frac{a^2}{4}+\frac{a^2}{4}.a^2+a^2.2a^2}}=\frac{a\sqrt{22}}{11}.\)

a: (SBD) giao (ABCD)=BD
SO vuông góc BD
AO vuông góc BD
=>((SBD);(ABCD))=góc SOA
b: (SCD) giao (SAD)=SD
Kẻ AH vuông góc SC
ΔSDC vuông tại D
Kẻ DK vuông góc SC
Qua H kẻ HF//DK
=>Góc cần tìm là góc AHF

1.SA \(\perp\)AB , SA\(\perp\)AD =>SAB vuông tại A, SAD vuông tại A
\(\begin{cases}AB\perp BC\left(hvABCD\right)\\SA\perp BC\left(SA\perp mpABCD\right)\end{cases}\) =>(SAB)\(\perp\)BC =>SB\(\perp\)BC =>SBC vuông tại B
\(\begin{cases}AD\perp CD\\SA\perp CD\end{cases}\) =>(SAD)\(\perp\)CD =>SD\(\perp\)CD =>SCD vuông tại D

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
\(AC=\sqrt{AD^2+CD^2}=a\sqrt{2}\)
\(BC=\sqrt{BE^2+CE^2}=a\sqrt{2}\)
\(\Rightarrow AC^2+BC^2=AB^2\Rightarrow AC\perp BC\)
\(\Rightarrow BC\perp\left(SAC\right)\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\)
b.
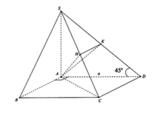
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=30^0\Rightarrow SA=AD.tan30^0=\dfrac{a\sqrt{3}}{3}\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Qua S kẻ đường thẳng d song song AD
Do \(AD||CE\) \(\Rightarrow\) d là giao tuyến (SAD) và (SCE)
Mà \(d\perp\left(SAB\right)\Rightarrow\widehat{ASE}\) là góc giữa (SAD) và (SCE)
\(AE=\dfrac{AB}{2}=a\)
\(tan\widehat{ASE}=\dfrac{AE}{SA}=\sqrt{3}\Rightarrow\widehat{ASE}=60^0\)