Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Ta có: A B 2 + A C 2 = B C 2 ( 6 2 + 8 2 = 10 2 = 100 )
Suy ra: tam giác ABC vuông tại A
⇒ AB ⊥ AC
* Lại có: MN ⊥ AB nên MN // AC.
* Vì MN // AC và M là trung điểm của BC nên N là trung điểm của AB.
Khi đó, MN là đường trung bình của tam giác ABC .
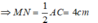
Chọn đáp án A

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành

a) Học sinh tự làm
b) Chứng minh A N 1 2 N C ⇒ S A M E = S A E N ⇒ E M = E N
hay E là trung điểm MN.
c) Chứng minh được EG//HF và HE/FG nên EHFG là hình bình hành; Mặt khác BM ^ NC (do AB ^ AC)
Suy ra EHFG là hình chữ nhật


Bài 1:

Áp dụng tính chất đường phân giác của tam giác ta có:
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{18}=\frac{2}{3}\)
\(\Rightarrow\frac{BD}{2}=\frac{DC}{3}=\frac{BD+DC}{2+3}=\frac{BC}{5}\Rightarrow\frac{BD}{BC}=\frac{2}{5}\)
Kẻ \(DK//BE\left(K\in AC\right)\text{ ta có:}\)
\(\frac{AE}{EK}=\frac{AI}{ID}=2;\frac{EK}{EC}=\frac{BD}{BC}=\frac{2}{5}\)
Do đó:\(\frac{AE}{EK}\cdot\frac{EK}{EC}=\frac{AE}{EC}=\frac{2}{5}.2=\frac{4}{5}\)
b)\(\text{Ta có:}\)
\(\frac{AE}{EC}=\frac{4}{5}\Rightarrow\frac{AE}{4}=\frac{EC}{5}=\frac{AE+EC}{4+5}=\frac{AC}{9}=\frac{18}{9}=2\)
\(\Rightarrow AE=8cm,EC=10cm\)
bn ơi bài 1 ý a) chỉ có thể tính tỉ lệ thôi ko tính đc ra số hẳn đâu
Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{BC}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Ta có: AB=AC
\(AM=MB=\dfrac{AB}{2}\)(M là trung điểm của AB)
\(AN=NC=\dfrac{AC}{2}\)(N là trung điểm của AC)
Do đó: \(AM=MB=AN=NC=\dfrac{AB}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Kẻ AH\(\perp\)MN tại H
Ta có: AH\(\perp\)MN
CE\(\perp\)MN
Do đó: AH//CE
Ta có: ΔAMN cân tại A
mà AH là đường cao
nên H là trung điểm của MN
=>\(HM=HN=\dfrac{MN}{2}=2\left(cm\right)\)
Ta có: ΔAHN vuông tại H
=>\(AH^2+HN^2=AN^2\)
=>\(AH^2+2^2=5^2\)
=>\(AH^2=25-4=21\)
=>\(AH=\sqrt{21}\left(cm\right)\)
Xét ΔNAH vuông tại H và ΔNCE vuông tại E có
NA=NC
\(\widehat{ANH}=\widehat{CNE}\)
Do đó: ΔNAH=ΔNCE
=>\(AH=CE=\sqrt{21}\left(cm\right)\)