Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) ACB=60 =>ACO đều => S ACO = 5 căn 3
S hình quạt AOC=(pi*5^2*60)/180
d) vì BC không đổi => S ABC max khi đường cao hạ từ A max => khi A chính giữa nữa dg tròn

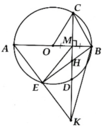
a, Chứng minh được ∆COD đều => A M B ^ = 60 0
b, A B C ^ = 30 0 => A O C ^ = 60 0 => l A C ⏜ = πR 3


`a)` Ta có: `\hat{AHI}=\hat{AKI}=90^o`
`=>` Tứ giác `AHIK` nội tiếp đường tròn đường kính `AI`
`b)` Ta có: `\hat{COB}=2\hat{CAB}` (cùng chắn cung `BC`)
`=>\hat{COB}=2.60^o =120^o=[2\pi]/3(rad)`
`=>` Độ dài cung `BC` nhỏ là: `l=\hat{COB}.R=[2\pi R]/3`
`=>` Diện tích hình quạt giới hạn bởi `2` bán kính `OB;OC` và cung nhỏ `BC` là:
`S=[lR]/2=[R^2]/3`

a: góc AHI=góc AKI=90 độ
=>AHIK nội tiếp
b: góc BOC=2*60=120 độ
\(S_{quạtBC}=pi\cdot R^2\cdot\dfrac{120}{360}=\dfrac{1}{3}\cdot pi\cdot R^2\)

2: ΔABC vuông tại A nội tiếp (O)
=>O là trung điểm của BC
BC=căn 6^2+8^2=10cm
=>OB=OC=10/2=5cm
S=5^2*3,14=78,5cm2

a: ΔABC vuông tại A
=>A nằm trên đường tròn đường kính BC
=>A thuộc (O)
b: Xét ΔABC vuông tại A có \(cosABC=\frac{AB}{BC}=\frac36=\frac12\)
nên \(\hat{ABC}=60^0\)
ΔABC vuông tại A
mà AO là đường trung tuyến
nên \(OA=OC=OB=\frac{BC}{2}=3\left(\operatorname{cm}\right)\)
Xét (O) có \(\hat{ABC}\) là góc nội tiếp chắn cung AC
nên \(\hat{AOC}=2\cdot\hat{ABC}=2\cdot60^0=120^0\)
Diện tích hình quạt tròn AOC là:
\(S_{q\left(AOC\right)}=\frac{\pi\cdot R^2\cdot n}{360}=\frac{\pi\cdot3^2\cdot120}{360}=3\pi\)
Diện tích tam giác AOC là:
\(S_{AOC}=\frac12\cdot OA\cdot OC\cdot\sin AOC=\frac12\cdot3\cdot3\cdot\sin120=\frac{9\sqrt3}{4}\left(\operatorname{cm}^2\right)\)
Diện tích hình viên phân giới hạn bởi dây AC và cung AC là:
\(S_{vp\left(AOC\right)}=S_{q\left(AOC\right)}-S_{AOC}=3\pi-\frac{9\sqrt3}{4}\)