Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)xet tam giac abd va tam giac aed co
ab=ae
ad la canh chunggoc bad = goc ead
=>tam giác abd = ead
b)gọi i là giao điểm của ad và be
xét tam giác abi và tam giác aei có :
ab=ae
ad là cạnh chung
goc bai = góc eai
=> tam giác abi= tâm giác aei
=>ib=ie =>ad là đường trung trực của be
cho mk 3 đi mk giải tiếp cho, bài nay mk vừa mới kiểm tra
mk giải tiếp nè
theo câu a,b=>góc dbf= góc dec (kề bù do góc abd= aed)
xét tam giác bfd và ecd có
góc dbf= góc dec
bd=ed
bdf=edc
=> tam giác dbf= tam giác ecd
k cho mk đi.mk hứa mk tl hết cho mà

Hình tự vẽ
Chứng minh
Gọi giao điểm của AD và BE là F
Vì AD là phân giác của góc ABC => góc BAD=góc CAD
Xét tam giác BAF và tam giác CAF :
AB=AB(gt)
góc BAD=góc CAD(cmt)
ÀF chung
=> Tam giác BAF = tam giác CAF(c.g.c)
=>BF=CF( hai cạnh tương ứng) (*)
góc BFA = góc CFA ( hai góc tương ứng) (1)
mà góc BFA + góc CFA = 180 độ ( 2 góc kề bù) (2)
Từ (1) và (2) => góc BFA = góc CFA = 90 độ =>AD vuông góc với BE(**)
Từ (*) và (**) => AD là trung trực BE (ĐPCM)

a,
xét tam giác ABD và tam giác ADE có
AB=AE (gt)
GÓC A1= GÓC A2 ( ad là tia phân giác)
ad chung
=> tam giác abd = tam giác ade (c.g.c)
b, xét tam giác BAI và tam giác EAI có:
AB=AE(gt)
A1=A2 (ad là tia phân giác)
AI chung
=> tam giác BAI = tam giác EAI (c.g.c)
=> BI=IE (2 cạnh t,ứng)
vì BI=BE ( cmt) => AI là đường trung trực của BE
P/s: 2 phần kia bạn tự làm nhé ak cái I là BE cắt AD tại I

3:
Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
=>AB=AE và DB=DE
=>AD là trung trực của BE

a, xét tam giác ABD và tam giác AED có : AD chung
^BAD = ^EAD do AD là pg của ^BAC (gt)
AB = AE (gt)
=> tam giác ABD = tam giác AED (c-g-c)
b, tam giác ABD = tam giác AED (câu a)
=> ^ABD = ^AED (đn)
^ABD + ^DBF = 180
^AED + ^DEC = 180
=> ^DBF = ^DEC
xét tam giác FBD và tam giác CED có : BF = EC (gt)
DB = DE do tam giác ABD = tam giác AED (câu a)
=> tam giác FBD = tam giác CED (c-g-c)
c, tam giác FBD = tam giác CED (câu b)
=> ^BDF = ^EDC (đn)
B;D;C thẳng hàng => ^BDE + ^EDC = 180
=> ^BDE + ^BDF = 180
=> E;D;F thẳng hàng
d, AB = AE (gt) => A thuộc đường trung trực của BE (tc)
BD = DE (câu b) => D thuộc đường trung trực của BE (Tc)
=> AD là đường trung trực của BE
e, DF = DC do tam giác BDF = tam giác EDC (Câu b)
=> tam giác DFC cân tại D (đn)
=> ^DCF = (180 - ^FDC) : 2 (tc)
DB = DE (câu b) => tam giác DEB cân tại D (đn) => ^EBD = (180 - ^BDE) : 2 (tc)
^FDC = ^BDE (đối đỉnh)
=> ^DCF = ^EBD mà 2 góc này slt
=> BE // CF
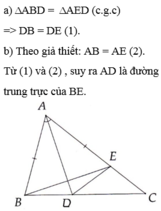
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó:ΔABD=ΔAED
Suy ra: DB=DE
b: Ta có: AB=AE
DB=DE
Do đó: AD là đường trung trực của BE
Xét ΔABD và ΔAED có
\(\widehat{BAD}=\widehat{EAD}\)
AB=AE
AD chung
==>ΔABD=ΔAED(c.g.c)
=>DB=DE(2 cạnh tg ứng)
Ta có: AB=AE(gt)
DB=DE(cmt)
==> AD là đường trung trực của BE