Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOBC có OB=OC
nên ΔOBC cân tại O
mà \(\widehat{CBO}=60^0\)
nên ΔOBC đều
Xét ΔOCM có
CB là đường trung tuyến
CB=OM/2
Do đó: ΔOCM vuông tại C
hay MC là tiếp tuyến của (O)

a, Vì OCB là tam giác đều nên BC=BO=BM=R
=> O C M ^ = 90 0 => MC là tiếp tuyến (O;R)
b, Ta có: O M 2 = O C 2 + M C 2
=> M C 2 = 3 R 2

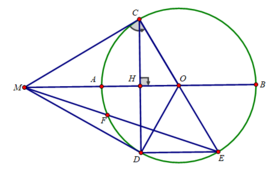
b) Ta có: OM = OA + AM = R + R = 2R
Xét tam giác MCO vuông tại C, CH là đường cao có:
MO 2 = MC 2 + OC 2
![]()
CH.OM = CM.CO
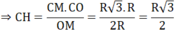
Lại có: CD = 2CH ⇒ CD = R 3
Tam giác CDE nội tiếp (O) có CE là đường kính nên ΔCDE vuông tại D
Theo định lí Py ta go ta có:
CE 2 = CD 2 + DE 2
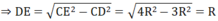
Câu 1:
a: Gọi H là giao điểm của OC và AB
Xét ΔOAB có OA=OB
nên ΔOAB cân tại O
mà OH là đường cao
nên OH là phân giác của góc AOB
Xét ΔCAO và ΔCBO có
OA=OB
\(\widehat{COA}=\widehat{COB}\)
OC chung
Do đo: ΔCAO=ΔCBO
Suy ra: \(\widehat{CAO}=\widehat{CBO}=90^0\)
=>CB là tiếp tuyến của (O)
b: AB=24cm nên AH=12cm
\(OH=\sqrt{15^2-12^2}=9\left(cm\right)\)
Xét ΔOAC vuông tại A có AH là đường cao
nên \(OH\cdot OC=OA^2\)
hay OC=25(cm)