Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) OBKC là hình bình hành (BK//OC,KC//OB) mà BOC=900 (vì BD _|_ AC do ABCD là hình thoi)
=>OBKC là hình chữ nhật
b) OBKC là hình chữ nhật (cmt) => OK=BC
mà BC=AB (ABCD là hình thoi)
=>AB=OK
c) Để hình chữ nhật OBKC là hình vuông <=> OB=OC
<=> AC=BD (vì OA=OC do O là tr.điểm AC trong hình thoi ABCD và OB=OC do O là tr.điểm BD)
Vậy hình thoi ABCD là hình vuông thì OBKC là hình vuông
nhầm chút,hình thoi ABCD có AC=BD thì OBKC là hình vuông nhé bn!

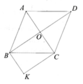
A B D C O K
a) tứ giác OBKC có BK // AC (GT) hay BK // OC
CK // BD (gt) hay CK // BO
=> OBKC là HBH ( vì là tứ giác có các cạnh đối //)
^BOC = 90ĐỘ (T/C Hthoi)
=> OBKC là HCN (vì là HBH có 1 góc vuông)
b) OBKC là HCN => OK = BC (t/c HCN) (1)
ABCD là Hthoi (gt) => AB = BC (t/c Hthoi) (2)
từ (1) và (2) => OK = AB
c) Hthoi ABCD cần ĐK ^A = 90ĐỘ để OBKC là Hvuông

Bài 2:
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trug điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
=>ΔABC vuông tại A

a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông

A) xét tứ giác OCKB :có BK song song với OC( vì BK song song với AC)
: có CK song song với OB ( vì CK song song vớiOB)
Từ hai điều kiện trên ta kết luận tứ giác OCKB là hình bình hành
mà ta lạ có góc COB=90 độ
vậy tứ giác OCKC là hình chữ nhật
B) Ta có : BK song song với OA ( vì BK song song song với AC)
Hơn nữa BK lại bằng OC ( vì OCBK là hình chữ nhật)
Mà OC lại bằng OA suy ra BK=OA
từ những điều kiện trên suy ra tứ giác ABKO là HBH
vậy AB=OK
C)nếu cần tìm điều kiện ở tứ giác ABCD để thỏa mãn tứ giác OBKC là hình vuông thì ta sẽ chọn điều kiện đó là
tứ giác ABCD là hình vuông
Bài 1.
Ta có: \(\left\{{}\begin{matrix}\widehat{COB}=90^0\left(ABCD.là.hình.thoi\right)\\\widehat{OBK}=90^0\left(BK.song.songAC\right)\\\widehat{OCK}=90^0\left(CK.song.song.BD\right)\end{matrix}\right.\) nên OBKC là hình chữ nhật.
b. Ta có: BK=OC (OBKC là hcn)
Mà OC=OA (ABCD là hình thoi)
=> BK=OA
Mà BK//OA (O thuộc AC)
=> ABKO là hình bình hành.
=> AB=OK
c. Để OBKC là hình vuông thì OC=OB.
=> Tam giác OCB vuông cân.
=> ABCD là hình vuông.
Bài 2.
a. Ta có: BC=AD (ABCD là hbh)
Mà E,F là trung điểm BC,AD => BE=EC=AF=FD
Ta lại có: BC=2AB => BC=2CD => BE=EC=AF=FD=CD
=> EC=FD=CD.(1)
Mà EF là đường trung bình của ABCD (E,F là trung điểm BC,AD)
=> EF=CD (2)
Từ (1),(2) => ECDF là hình thoi.
b. Ta có: góc DAB =60 độ => góc FDC=120 độ
Mà DE là phân giác của góc FDC (ECDF là hình thoi)
=> góc FDE=60 độ.
=> góc FDE=góc FAB=60 độ
Mà BE//AD (E thuộc BC)
=> BEDA là hình thang cân.
c. Chứng minh tương tự 2 câu a,b trên, ta có: ABEF là hình thoi và góc BAE = 30 độ.
=> góc AEF=góc BAE=30 độ.
Ta có: \(\widehat{AED}=\widehat{AEF}+\widehat{FED}=30^0+60^0=90^0\)
@Rain Tờ Rym Te