Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

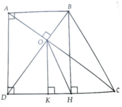
a, Tính được DB=15cm. A D B ^ ≈ 37 0 ; A B D ^ ≈ 53 0
b, Tính được AO=7,2cm, DO=9,6cm và AC=20cm
c, Kẻ OK ⊥ DC tại K
DH=AB=9cm, DC=16cm, DK=5,76cm và OK=7,68cm
Từ đó S D O H = O K . D H 2 = 7 , 68 . 9 2 = 34,56 c m 2

a: Xét ΔABM vuông tại A và ΔDMC có
BA/DM=AM/CD
nên ΔABM đồng dạng với ΔDMC
b: Ta có: ΔABM đồng dạng với ΔDMC
nên góc AMB=góc DCM
=>góc AMB+góc DMC=góc DCM+góc DMC=90 độ
=>góc BMC=90 độ
=>ΔBMC vuông tại M
c: \(S=MB\cdot\dfrac{MC}{2}=10\cdot\dfrac{20}{2}=100\left(cm^2\right)\)

a: Xét ΔABM vuông tại A và ΔDMC có
BA/DM=AM/CD
nên ΔABM đồng dạng với ΔDMC
b: Ta có: ΔABM đồng dạng với ΔDMC
nên góc AMB=góc DCM
=>góc AMB+góc DMC=góc DCM+góc DMC=90 độ
=>góc BMC=90 độ
=>ΔBMC vuông tại M
c: \(S=MB\cdot\dfrac{MC}{2}=10\cdot\dfrac{20}{2}=100\left(cm^2\right)\)

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

b) xét ∆ABC có AD là đường phân giác của góc A
=>BD/AB=DC/AC ( tính chất)
Áp dụng tính chất dãy tỉ số bằng nhau , được :
BD/AB=DC/AC=BD/6=DC/8=(BD+DC)/(6+8)=BD/14=10/14=5/7
==>BD=6×5:7≈4,3
==>DC=10-4,3≈5,7
a,Áp dụng định lý Pi-ta-go vào tam giác ABC => tam giác ABC vuông tại A=> AH vuông góc vs BC
=> tam giác ABC đồng dạng vs tam giác HAC ( g.c.g)
b, Vì tam giác ABC vuông tại A nên ta có hệ thức: AC2=BC . HC => đpcm
c, có AD là tia phân giác của tam giác ABC => BD=CD=BC/2= 5cm
a) Xét tam giác AOD và tam giác BAD có:
{Dˆ:chungAOˆD=DAˆB=90{D^:chungAO^D=DA^B=90⇒ΔAOD≀ΔBAD(g.g)⇒ΔAOD≀ΔBAD(g.g)
b) Ta có: DAˆO=ABˆD=ABˆO(ΔAOD≀ΔBAD)DA^O=AB^D=AB^O(ΔAOD≀ΔBAD)
Và AOˆD=AOˆB=90AO^D=AO^B=90 (2 đường chéo vuông góc tại O)
Do đó ΔAOD≀ΔBOA(g.g)ΔAOD≀ΔBOA(g.g)
⇒ADAB=ODAO⇒ADAB=ODAO (1)
Lại có: {DAˆO:chungAOˆD=ADˆC=90{DA^O:chungAO^D=AD^C=90⇒ΔADC≀ΔAOD(g.g)⇒ΔADC≀ΔAOD(g.g)
⇒CDOD=ADAO⇔CDAD=ODAO⇒CDOD=ADAO⇔CDAD=ODAO (2)
Từ (1);(2)⇒ADAB=CDAD⇒AD2=AB⋅CD⇒ADAB=CDAD⇒AD2=AB⋅CD
c) Ta có: AB song song với DC (ABCD là hình thang)
⇒ABˆO=ODˆC(slt)⇒AB^O=OD^C(slt)
Và AOˆB=DOˆC(đ2)AO^B=DO^C(đ2)
Do đó ΔOCD≀ΔOAB(g.g)ΔOCD≀ΔOAB(g.g)
⇒k=OCOA=CDAB=94⇒k=OCOA=CDAB=94
⇒SΔOCDSΔOAB=k2=942=8116⇒SΔOCDSΔOAB=k2=942=8116
Vậy........................
Δ : tam giác. Chúc bạn học tốt nhé!