Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

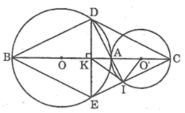
Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại D
Suy ra: AD ⊥ BD
Tứ giác BDCE là hình thoi nên EC // BD
Suy ra: EC ⊥ AD (1)
Tam giác AIC nội tiếp trong đường tròn (O’) có AC là đường kính nên vuông tại I
Suy ra: AI ⊥ CE (2)
Từ (1) và (2) suy ra AD trùng với AI
Vậy D, A, I thẳng hàng.

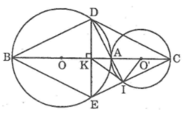
Vì đường tròn (O) và (O’) tiếp xúc ngoài tại A nên O, A và O’ thẳng hàng
Ta có: KB = KC (gt)
Trong đường tròn (O) ta có:
AB ⊥ DE tại K
Suy ra: KD = KE (đường kính vuông góc với dây cung)
Tứ giác BDCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có: BC ⊥ DE
Suy ra tứ giác BDCE là hình thoi.

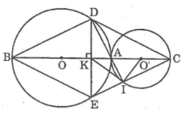
Tam giác DIE vuông tại I có IK là trung tuyến thuộc cạnh huyền DE nên: KI = KD = (1/2).ED (tính chất tam giác vuông)
Suy ra tam giác IKD cân tại K


a) Vì đường tròn (O) và (O') tiếp xúc ngoài tại A nên O, A và O’ thẳng hàng.
Ta có: MB = MC (M là TĐ của BC)
Xét (O) ta có: DE vg góc BC (gt)
mà M là TĐ của BC
Suy ra : M là TĐ của DE ( đường kính vuông góc với dây cung)
Xét TG BDCE có 2 đường chéo DE và BC cắt nhau tại trung điểm M của mỗi đường
Suy ra: BDCE là hình bình hành.
(Bổ sung)
Lại có: BC ⊥ DE
Suy ra tứ giác BDCE là hình thoi


A B C D E K I O' O N
a/
Ta có
\(BC\perp DE\left(gt\right)\left(1\right)\Rightarrow DK=EK\) (trong hình tròn, đường kính vuông góc với dây cung thì chia đôi dây cung)
AK=CK (gt)
=> BDCE là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh) (2)
Từ (1) Và (2) => BDCE là hình thoi (Hình bình hành có 2 đường chéo vuông góc là hình thoi)
b/ Nối C với I và C với E
Ta có CE//BD (cạnh đối hình thoi)
Xét (O) có
\(\widehat{BDA}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow BD\perp DI\)
Xét (O') có
\(\widehat{AIC}=90^o\)(góc nt chắn nửa đường tròn) \(\Rightarrow CI\perp DI\)
=> CI//BD
Như vậy CE và CI cùng // với BD \(\Rightarrow CE\equiv CI\) (Từ 1 điểm bên ngoài đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho) => E, I, C thẳng hàng
c/
Ta có
\(DE\perp BC\left(gt\right)\Rightarrow\widehat{DKC}=90^o\)
\(\widehat{AIC}=90^o\left(cmt\right)\)
=> K và I cùng nhìn CD dưới 2 góc bằng nhau và \(=90^o\) => CDKI là tứ giác nội tiếp
\(\Rightarrow\widehat{KID}=\widehat{KCD}\) (góc nt cùng chắn cung KD) (3)
Xét tg vuông CDK và tg vuông CEK có
DK=EK (gt); CK chung => tg CDK = tg CEK (2 tg vuông có 2 cạnh góc vuông = nhau)
\(\Rightarrow\widehat{KCD}=\widehat{KCE}\) (4)
Xét tg O'IC có
O'I=O'C=r => tg O'IC cân tại O'
\(\Rightarrow\widehat{KCE}=\widehat{O'IC}\) (5)
Từ (3) (4) (5) \(\Rightarrow\widehat{KID}=\widehat{O'IC}\)
Mà \(\widehat{O'IC}+\widehat{AIO'}=\widehat{AIC}=90^o\)
\(\Rightarrow\widehat{KID}+\widehat{AIO'}=\widehat{KIO'}=90^o\Rightarrow KI\perp O'I\)
=> KI là tiếp tuyến của (O')