Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2
Kẻ D doi xung voi A qua Ox
E doi xung voi A qua Oy
Goi B' la 1 diem bat ki tren Ox,C' la 1 diem bat ki tren Oy
Do Ox la duong trung truc cua AD
=> BA=BD,B'A=B'A
Tuong tu=> C'A=C'E,CA=CE
Ta co
PABC=AB+BC+AC
Ma AB=BD.AC=CE
=>PABC=BC+BD+CE=ED
lai co B'D+B'E\(\ge ED\)
B'C'\(\ge B'E\)
=> B'D+B'C'+C'E\(\ge ED\)
=>PAB'C'\(\ge P_{ABC}\)
Dau ''='' xay ra khi B'\(\equiv B,C'\equiv C\)

a: Ta có: AE+EB=AB
AF+FC=AC
mà AB=AC
và EB=FC
nên AE=AF
hay A nằm trên đường trung trực của FE(1)
Xét ΔEBH và ΔFCH có
EB=FC
\(\widehat{B}=\widehat{C}\)
BH=CH
Do đó: ΔEBH=ΔFCH
Suy ra: HE=HF
hay H nằm trên đường trung trực của FE(2)
Từ (1) và (2) suy ra E và F đối xứng nhau qua AH

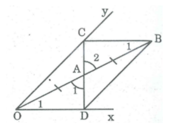
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.

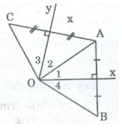
Vì B đối xứng với A qua trục Ox nên Ox là đường trung trực của đoạn AB.
⇒ OA = OB (tính chất đường trung trực) (1)
Vì C đối xứng với A qua trục Oy nên Oy là đường trung trực của đoạn AC.
⇒ OA = OC (tính chất đường trung trực) (2)
Từ (l) và (2) suy ra: OB = OC.

Gọi giao điểm của MN và Ox là điểm A; giao điểm của MN và Oy là điểm B.
Ta có: N là điểm đối xứng với M qua Ox (gt).
O \(\in\) Ox.
=> \(\left\{{}\begin{matrix}OA\perp MN.\\\text{ON = OM.(1)}\end{matrix}\right.\)
Ta có: P là điểm đối xứng với M qua Oy (gt).
O \(\in\) Oy.
=> \(\left\{{}\begin{matrix}OB\perp MP.\\\text{OM = OP.(2)}\end{matrix}\right.\)
Từ (1) và (2) => OP = ON = OM.
Xét tam giác NOM có: ON = OM (cmt).
=> Tam giác NOM cân tại O.
Mà OA là đường cao (do OA vuông góc MN).
=> OA là phân giác của ^NOM (Tính chất các đường trong tam giác cân).
=> ^NOA = ^AOM.
Xét tam giác MOP có: OP = OM (cmt).
=> Tam giác MOM cân tại O.
Mà OB là đường cao (do OB vuông góc MP).
=> OB là phân giác của ^MOP (Tính chất các đường trong tam giác cân).
=> ^MOB = ^BOP.
Ta có: ^NOA + ^AOM + ^MOB + ^BOP.
= 2. ^AOM + 2. ^MOB.
= 2. (^AOM + ^MOB).
= 2. ^AOB.
= 2. 90o = 180o.
=> 3 điểm N; O; P thẳng hàng.
Mà OP = ON (cmt).
=> O là trung điểm của NP.
=> P và N đối xứng nhau qua O (đpcm).

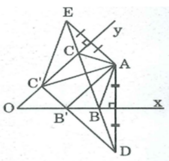
Cách dựng:
- Dựng điểm D đối xứng với A qua Ox
- Dựng điểm E đối xứng với A qua Oy
Nối DE cắt Ox tại B, Oy tại C
Tam giác ABC là tam giác có chu vi nhỏ nhất
Vì ∠ (xOy) < 90 0 nên DE luôn cắt Ox và Oy do đó ∆ ABC luôn dựng được.
Chứng minh:
Chu vi ∆ ABC bằng AB + BC + AC
Vì D đối xứng với A qua Ox nên Ox là trung trực của AD
⇒ AB = BD (tính chất đường trung trực)
E đối xứng với A qua Oy nên Oy là trung trực của AE
⇒ AC = CE (tính chất đường trung trực)
Suy ra: AB + BC + AC = BD + BC + BE = DE (1)
Lấy B' bất kì trên Ox, C' bất kì trên tia Oy. Nối C'E, C'A, B'A, B'D.
Ta có: B'A = B'D và C'A = C'E (tính chất đường trung trực)
Chu vi ∆ AB'C' bằng AB'+ AC’ + B'C'= B'D+C’E+ B'C' (2)
Vì DE ≤ B'D + C’E+ B'C' (dấu bằng xảy ra khi B' trùng B, C' trùng C) nên chu vi của ∆ ABC ≤ chu vi của ∆ A'B'C'
Vậy ∆ ABC có chu vi bé nhất.