OLM ưu đãi đặc biệt gói SVIP 18 THÁNG dành cho nhà trường, đăng kí ngay!

OLM tuyển CTV cộng đồng hỏi đáp, đăng kí ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
NC
nguyễn con bò
21 tháng 3 2020 - olm
Bài 1: Cho góc xOy bằng 100 0 , điểm H thuộc tia phân giác của góc đó. Đườngvuông góc với OH tại H cắt các tia Ox, Oy theo thứ tự ở A và B.a. CMR: HA = HB, OA = OBb. Trên nửa mặt phẳng không chứa O bờ AB, vẽ tam giác đều ABC. CMR bađiểm O, H, C thẳng hàng.c. Trên cạnh BC lấy điểm E sao cho BE = BO. CMR: AB = OE.d. Trên cạnh AC lấy điểm I sao cho AI = AH. Tam giác AIH là tam giác gì? Vìsao?e. Cho AH = 1cm. Tính...
Đọc tiếp

Bài 1: Cho góc xOy bằng 100 0 , điểm H thuộc tia phân giác của góc đó. Đường
vuông góc với OH tại H cắt các tia Ox, Oy theo thứ tự ở A và B.
a. CMR: HA = HB, OA = OB
b. Trên nửa mặt phẳng không chứa O bờ AB, vẽ tam giác đều ABC. CMR ba
điểm O, H, C thẳng hàng.
c. Trên cạnh BC lấy điểm E sao cho BE = BO. CMR: AB = OE.
d. Trên cạnh AC lấy điểm I sao cho AI = AH. Tam giác AIH là tam giác gì? Vì
sao?
e. Cho AH = 1cm. Tính HC.

LÀM ƠN NHA CẢM ƠN NHA

CẢM ƠN RỒI ĐÓ LÀM HỘ NHAAAAAAAAAA
#Hỏi cộng đồng OLM #Toán lớp 7
0
T
thanhmai
5 tháng 3 2020 - olm
bài 7 : cho góc xOy =100 độ , điểm H thuộc tia phân giác của góc đó . đường vuông góc với OH tại H cắt các tia Ox , Oy theo thứ tự ở A và B .a) CMR HA=HB, OA=OB b) trên nửa mặt phẳng không chứa O bờ AB , vẽ tam giác đều ABC , CMR ba điểm O,H,C thẳng hàng c) trên cạnh BC lấy điểm E sao cho BE=BO , CMR AB=OEd) trên cạnh AC lấy điểm I sao cho AI=AH . Tam giác AIH là tam giác gì ? vì sao ?e) cho AH = 1cm . tính...
Đọc tiếp

bài 7 : cho góc xOy =100 độ , điểm H thuộc tia phân giác của góc đó . đường vuông góc với OH tại H cắt các tia Ox , Oy theo thứ tự ở A và B .

a) CMR HA=HB, OA=OB 

b) trên nửa mặt phẳng không chứa O bờ AB , vẽ tam giác đều ABC , CMR ba điểm O,H,C thẳng hàng 

c) trên cạnh BC lấy điểm E sao cho BE=BO , CMR AB=OE

d) trên cạnh AC lấy điểm I sao cho AI=AH . Tam giác AIH là tam giác gì ? vì sao ?

e) cho AH = 1cm . tính HC
#Hỏi cộng đồng OLM #Toán lớp 7
2
NA
Ngọc Ánh
5 tháng 3 2020

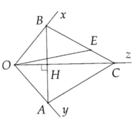
Bạn tự vẽ hình nha!

a) Vì tia OH là tia phân giác của \(\widehat{xOy}\)

\(\Rightarrow\) \(\widehat{xOH}\)=\(\widehat{yOH}\)hay \(\widehat{AOH}\)=\(\widehat{BOH}\)\((\)vì A\(\in\)Ox,B\(\in\)Oy\()\)

Xét tam giác AOH và tam giác BOH, có:

         \(\widehat{AOH}\)=\(\widehat{BOH}\)

          OH chung

           \(\widehat{OHA}\)=\(\widehat{OHB}\)(=\(^{90^0}\))

\(\Rightarrow\)Tam giác AOH= Tam giác BOH (g-c-g)

\(\Rightarrow\)\(\hept{\begin{cases}HA=HB\\OA=OB\end{cases}}\)

Vậy....

Đúng(0)
NT
Nguyen Thi Xuan
5 tháng 4 2020

Phần b,c,d,e đâu rồi hả bạn Ngọc Ánh 

Đúng(0)
NT
Nguyen Thi Xuan
4 tháng 4 2020 - olm
Bài 1:Cho góc xOy=100 độ,điểm H thuộc tia phân giác của góc đó.Đường vuông góc với OH tại H cắt tia Ox,Oy theo thứ tự ở A,B a) Chứng minh rằng: HA=HB;OA=OB b) Trên nửa mặt phẳng không chứa O bờ AB, vẽ tam giác đều ABC.Chứng minh rằng AB=OE c) Trên cạnh BC lấy điểm E sao cho BE=BO. Chứng minh rằng AB=OE d) Trên cạnh AC lấy điểm I sao cho AI=AH.Tam giác AIH là tam giác gì? Vì sao? e) Cho AH=1 cm. Tính độ dài...
Đọc tiếp

Bài 1:Cho góc xOy=100 độ,điểm H thuộc tia phân giác của góc đó.Đường vuông góc với OH tại H cắt tia Ox,Oy theo thứ tự ở A,B a) Chứng minh rằng: HA=HB;OA=OB b) Trên nửa mặt phẳng không chứa O bờ AB, vẽ tam giác đều ABC.Chứng minh rằng AB=OE c) Trên cạnh BC lấy điểm E sao cho BE=BO. Chứng minh rằng AB=OE d) Trên cạnh AC lấy điểm I sao cho AI=AH.Tam giác AIH là tam giác gì? Vì sao? e) Cho AH=1 cm. Tính độ dài HC

vẽ hình giúp với nhé đừng lười vẽ nhé!help me
#Hỏi cộng đồng OLM #Toán lớp 7
0
NN
Nguyễn Ngọc Minh Hương
20 tháng 2 2016 - olm
Mong các bạn giải giúp mình:Cho góc xOy=1000. H thuộc tia phân giác của góc đó. Đường vuông góc với OH tại H cặt Ox, Oy lần lượt tại A và Ba) CM:HA=HB, OA=OBb) Trên nửa mặt phẳng bờ AB. Vẽ tam giác đều ABC. CM:O, H, C thẳng hàngc) Trên cạnh BC lấy điểm E sao cho BE=BO. CM: AB=OEd) Trên cạnh AC lấy điểm I sao cho AI=AH. Tam giác AIH là tam giác gì? tại sao?e) cho AH=1cm. Tính...
Đọc tiếp

Mong các bạn giải giúp mình:

Cho góc xOy=1000. H thuộc tia phân giác của góc đó. Đường vuông góc với OH tại H cặt Ox, Oy lần lượt tại A và B

a) CM:HA=HB, OA=OB

b) Trên nửa mặt phẳng bờ AB. Vẽ tam giác đều ABC. CM:O, H, C thẳng hàng

c) Trên cạnh BC lấy điểm E sao cho BE=BO. CM: AB=OE

d) Trên cạnh AC lấy điểm I sao cho AI=AH. Tam giác AIH là tam giác gì? tại sao?

e) cho AH=1cm. Tính HC
#Hỏi cộng đồng OLM #Toán lớp 7
0
TT
Tiểu Thiên Bình
20 tháng 2 2016 - olm
Mong các bạn giải giúp mình:Cho góc xOy=1000. H thuộc tia phân giác của góc đó. Đường vuông góc với OH tại H cặt Ox, Oy lần lượt tại A và Ba) CM:HA=HB, OA=OBb) Trên nửa mặt phẳng bờ AB. Vẽ tam giác đều ABC. CM:O, H, C thẳng hàngc) Trên cạnh BC lấy điểm E sao cho BE=BO. CM: AB=OEd) Trên cạnh AC lấy điểm I sao cho AI=AH. Tam giác AIH là tam giác gì? tại sao?e) cho AH=1cm. Tính...
Đọc tiếp

Mong các bạn giải giúp mình:

Cho góc xOy=1000. H thuộc tia phân giác của góc đó. Đường vuông góc với OH tại H cặt Ox, Oy lần lượt tại A và B

a) CM:HA=HB, OA=OB

b) Trên nửa mặt phẳng bờ AB. Vẽ tam giác đều ABC. CM:O, H, C thẳng hàng

c) Trên cạnh BC lấy điểm E sao cho BE=BO. CM: AB=OE

d) Trên cạnh AC lấy điểm I sao cho AI=AH. Tam giác AIH là tam giác gì? tại sao?

e) cho AH=1cm. Tính HC
#Hỏi cộng đồng OLM #Toán lớp 7
0
L
Linh
17 tháng 7 2023 - olm

Cho góc xOy bằng 100 độ, điểm H thuộc tia phân giác của góc đó. Đường vuông góc với OH tại h cắt các tia Ox, Oy theo thứ tự ở A và B

a, CMR: HA=HB ; OA = OB

b, Trên nửa mặt phẳng không chứa O bờ AB, vẽ tam giác đều ABC. CMR ba điểm O, H, C thẳng hàng
#Hỏi cộng đồng OLM #Toán lớp 7
1
KK
✎﹏Kim Kim✧❤‿✶🌈(*•.¸♡ţęąɱ ƒŗęę ƒįŗę...
17 tháng 7 2023

Ta có OH\(\perp\)AB 

=>OH là đường cao

Mà HC là đường cao của ∆OAB

=>∆OAB là ∆ cân

=> Oh cũng là đường trung trực của AB 

=> HA=HB (1)

Xét ∆OAB có: OA=OB (2)

Từ (1) và (2) =>HA=HB; OA=OB(đpcm)

b, Ta có HA=HB(cmt) 

=>HC là trung tuyến của ∆ABC

Mà ∆ ABC là ∆ đều

=>HC là đường trung trực của AB(2)

Từ (1);(2)=> O;H;C thẳng hàng (đpcm)

 

Đúng(0)
HT
Hoàng Thị Mỹ Lệ
6 tháng 7 2015 - olm
Cho góc xOy =100 độ.Điểm H thuộc tia phân giác của góc đó.Đường vuông góc với OH tại H cắt Ox,Oy lần lượt tại A và Ba)Chứng minh rằng: HA=HB,OA=OBb)Trên nửa mặt phẳng bờ k chứa O bờ AB,vẽ tam giác ABC đều.CMR:O,H,C thẳng hàngc)Trên BC lấy E sao cho BE=BO.cmr:AB=OEd)Trên AC lấy I sao cho AI=AH.Tam giác AIH là tam giác gì?Vì sao?e)Cho AH=1cm,tính HC? Mọi người giúp mình với! Mơn m.n...
Đọc tiếp

Cho góc xOy =100 độ.Điểm H thuộc tia phân giác của góc đó.Đường vuông góc với OH tại H cắt Ox,Oy lần lượt tại A và B

a)Chứng minh rằng: HA=HB,OA=OB

b)Trên nửa mặt phẳng bờ k chứa O bờ AB,vẽ tam giác ABC đều.CMR:O,H,C thẳng hàng

c)Trên BC lấy E sao cho BE=BO.cmr:AB=OE

d)Trên AC lấy I sao cho AI=AH.Tam giác AIH là tam giác gì?Vì sao?

e)Cho AH=1cm,tính HC?

 

Mọi người giúp mình với! Mơn m.n nhiều
#Hỏi cộng đồng OLM #Toán lớp 7
0
PT
Pham Trong Bach
2 tháng 7 2017
Cho góc xOy bằng 100 ° , tia Oz là tia phân giác góc xOy. Lấy điểm H thuộc tia Oz, đường thẳng vuông góc với OH tại H cắt các tia Ox, Oy lần lượt tại A, B.a) Chứng minh HA = HB, OA = OB.b) Tính số đo các góc của tam giác OAB.c) Trên tia Oz lấy điểm C sao cho H B C ^   =   60 ° . Chứng minh tam giác ABC đều.d)...
Đọc tiếp

Cho góc xOy bằng 100 ° , tia Oz là tia phân giác góc xOy. Lấy điểm H thuộc tia Oz, đường thẳng vuông góc với OH tại H cắt các tia Ox, Oy lần lượt tại A, B.

a) Chứng minh HA = HB, OA = OB.

b) Tính số đo các góc của tam giác OAB.

c) Trên tia Oz lấy điểm C sao cho H B C ^   =   60 ° . Chứng minh tam giác ABC đều.

d) Trên cạnh BC lấy điểm E sao cho BE = BO. Chứng minh AB = OE.

e) Cho AH = 1 cm. Tính độ dài HC.
#Hỏi cộng đồng OLM #Toán lớp 7
1
CM
Cao Minh Tâm
2 tháng 7 2017

Đúng(0)
NB
nguyễn bảo quỳnh
3 tháng 4 2020 - olm
Bài 2. Cho ABC có A = 120°. Tia phân giác của A cắt BC tại D. Tia phân giác củaADC cắt AC tại I. Gọi H, K, E lần lượt là hình chiếu của I trên đương thẳng AB,BC, AD. Chứng minh:a) AC là tia phân giác của DAH .b) IH = IKBài 5. Cho tam giác ABC vuông tại A. Từ một điểm K bất kì trên cạnh BC, vẽ KH AC (HAC). Trên tia đối của tia HK lấy điểm I sao cho HI = HK. Chứngminh:a) Chứng minh AB //HKb) Chứng minh KAH...
Đọc tiếp

Bài 2. Cho ABC có A = 120°. Tia phân giác của A cắt BC tại D. Tia phân giác của
ADC cắt AC tại I. Gọi H, K, E lần lượt là hình chiếu của I trên đương thẳng AB,
BC, AD. Chứng minh:
a) AC là tia phân giác của DAH .
b) IH = IK
Bài 5. Cho tam giác ABC vuông tại A. Từ một điểm K bất kì trên cạnh BC, vẽ KH
 AC (HAC). Trên tia đối của tia HK lấy điểm I sao cho HI = HK. Chứng
minh:
a) Chứng minh AB //HK
b) Chứng minh KAH IAH 
c) Chứng minh AKI cân
Bài 7. Cho ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao
cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh:
a) BE = CD b) BMD = CME
c) Đường vuông góc với OE tại E cắt Ox, Oy lần lượt tại M, N. Chứng minh
MN / / AC //BD.
Bài 8. Cho xOy . Lấy các điểm A,B thuộc tia Ox sao cho OA > OB. Lấy các điểm C, D
thuộc Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC
Chứng minh.:
a) AD = BC b) ABE = CDE
c) OE là tia phân giác của góc xOy
#Hỏi cộng đồng OLM #Toán lớp 7
4
AT
Anh Thư
24 tháng 4 2020

mik ngu hình lắm xin lỗi nha

Đúng(0)
LQ
Lương Quang Vinh
24 tháng 4 2020

ngu thì xen zô nói làm j

Đúng(1)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP