Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(n_{Zn}=\dfrac{26}{65}=0,4\left(mol\right)\)
\(n_{HCl}=\dfrac{18,25}{36,5}=0,5\left(mol\right)\)
PTHH :
a, \(Zn+2HCl\rightarrow ZnCl_2+H_2\uparrow\)
Trc p/u : 0,4 0,5
p/u: 0,25 0,5 0,25 0,25
sau p/u : 0,15 0 0,25 0,25
b, ----> sau p/ư ; Zn dư
\(m_{Zndư}=0,15.65=9,75\left(g\right)\)
PTHH :
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\uparrow\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\uparrow\)
Từ PTHH ta có , 1 mol Al sẽ cho ra 1,5 mol H2
1 mol Fe sẽ cho ra 1 mol H2
Mà Al lại có Khối lượng mol nhỏ hơn Fe
Vậy , nếu cho cùng 1 khối lượng 2 kim loại trên thì Al sẽ cho ra nhiều H2 hơn

a)
$Zn + H_2SO_4 \to ZnSO_4 + H_2(1)$
$2Al + 3H_2SO_4 \to Al_2(SO_4)_3 + 3H_2(2)$
$Fe + H_2SO_4 \to FeSO_4 + H_2(3)$
b)
Coi m Zn = m Al = m Fe = 100(gam)
\(n_{H_2(1)} = n_{Zn} = \dfrac{100}{65}(mol)\\ n_{H_2(2)} = \dfrac{3}{2}n_{Al} = \dfrac{3}{2}.\dfrac{100}{27} = \dfrac{100}{18}(mol)\\ n_{H_2(3)} = n_{Fe} = \dfrac{100}{56}(mol)\\\)
Ta thấy :
\(n_{H_2(1)} < n_{H_2(3)} < n_{H_2(2)}\) nên dùng kim loại Al cho được nhiều khí hidro nhất.
c) Coi $n_{H_2} = 1(mol)$
n Zn = n H2 = 1(mol) => m Zn = 1.65 = 65(gam)
n Al = 3/2 n H2 = 1,5(mol) => m Al = 1,5.27 = 40,5(gam)
n Fe = n H2 = 1(mol) => m Fe = 1.56 = 56(gam)
Vậy cùng một thể tích hidro thì Al có khối lượng nhỏ nhất
a, PT: \(Zn+H_2SO_4\rightarrow ZnSO_4+H_2\) (1)
\(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\) (2)
\(Fe+H_2SO_4\rightarrow FeSO_4+H_2\) (3)
b, Giả sử: mZn = mAl = mFe = a (g)
\(\Rightarrow\left\{{}\begin{matrix}n_{Zn}=\dfrac{a}{65}\left(mol\right)\\n_{Al}=\dfrac{a}{27}\left(mol\right)\\n_{Fe}=\dfrac{a}{56}\left(mol\right)\end{matrix}\right.\)
Theo PT: \(\left\{{}\begin{matrix}n_{H_2\left(1\right)}=n_{Zn}=\dfrac{a}{65}\left(mol\right)\\n_{H_2\left(2\right)}=\dfrac{3}{2}n_{Al}=\dfrac{a}{18}\left(mol\right)\\n_{H_2\left(3\right)}=n_{Fe}=\dfrac{a}{56}\left(mol\right)\end{matrix}\right.\)
⇒ Al cho nhiều khí H2 nhất.
c, Giả sử: nH2 (1) = nH2 (2) = nH2 (3) = b (mol)
Theo PT: \(\left\{{}\begin{matrix}n_{Zn}=n_{H_2\left(1\right)}=b\left(mol\right)\\n_{Al}=\dfrac{2}{3}n_{H_2\left(2\right)}=\dfrac{2}{3}b\left(mol\right)\\n_{Fe}=n_{H_2\left(3\right)}=b\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m_{Zn}=65b\left(g\right)\\m_{Al}=\dfrac{2}{3}b.27=18b\left(g\right)\\m_{Fe}=56b\left(g\right)\end{matrix}\right.\)
⇒ Khối lượng Al pư là nhỏ nhất.

a) Phương trình phản ứng:
Zn + H2SO4 → ZnSO4 + H2
Fe + H2SO4loãng → FeSO4 + H2
2Al+ 3H2SO4 → Al2(SO4)3 + 3H2
b) Giả sử cho cùng một khối lượng là a g kim loại kẽm sắt và nhôm
Zn + H2SO4 → ZnSO4 + H2 (1)
Fe + H2SO4loãng → FeSO4 + H2 (2)
2Al+ 3H2SO4 → Al2(SO4)3 + 3H2 (3)
Ta có 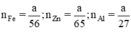
Theo pt nH2 (1) = nZn = 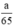 mol
mol
nH2 (2) = nFe = 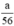 mol
mol
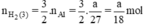
Như vậy ta nhận thấy 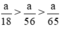 ⇒ nH2 (3) > nH2 (2) > nH2 (1)
⇒ nH2 (3) > nH2 (2) > nH2 (1)
Như vậy cho cùng một lượng kim loại tác dụng với axit H2SO4 loãng dư thì nhôm cho nhiều khí hidro hơn, sau đó đến sắt và ít nhất là kẽm
c) Nếu thu được cùng một lượng khí hidro thì khối lượng kim loại ít nhất là nhôm, sau đó đến sắt, cuối cùng là kẽm.

Bài 1:
a, PT: \(Zn+2HCl\rightarrow ZnCl_2+H_2\) (1)
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\) (2)
b, Giả sử: mZn = mAl = a (g)
\(\Rightarrow\left\{{}\begin{matrix}n_{Zn}=\dfrac{a}{65}\left(mol\right)\\n_{Al}=\dfrac{a}{27}\left(mol\right)\end{matrix}\right.\)
Theo PT: \(\left\{{}\begin{matrix}n_{H_2\left(1\right)}=n_{Zn}=\dfrac{a}{65}\left(mol\right)\\n_{H_2\left(2\right)}=n_{Al}=\dfrac{a}{27}\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow n_{H_2\left(1\right)}< n_{H_2\left(2\right)}\)
Vậy: Al cho nhiều khí H2 hơn.
c, Giả sử: nH2 (1) = nH2 (2) = b (mol)
Theo PT: \(\left\{{}\begin{matrix}n_{Zn}=n_{H_2\left(1\right)}=b\left(mol\right)\\n_{Al}=n_{H_2\left(2\right)}=b\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m_{Zn}=65b\left(g\right)\\m_{Al}=27b\left(g\right)\end{matrix}\right.\)
\(\Rightarrow m_{Zn}>m_{Al}\)
Vậy: Khối lượng Al đã pư nhỏ hơn.
Bài 2:
PT: \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
a, Ta có: \(n_{Fe}=\dfrac{11,2}{56}=0,2\left(mol\right)\)
\(n_{H_2SO_4}=\dfrac{9,8}{98}=0,1\left(mol\right)\)
Xét tỉ lệ: \(\dfrac{0,2}{1}>\dfrac{0,1}{1}\), ta được Fe dư.
Theo PT: \(n_{Fe\left(pư\right)}=n_{H_2SO_4}=0,1\left(mol\right)\)
\(\Rightarrow n_{Fe\left(dư\right)}=0,1\left(mol\right)\Rightarrow m_{Fe\left(dư\right)}=0,1.56=5,6\left(g\right)\)
b, Theo PT: \(n_{H_2}=n_{H_2SO_4}=0,1\left(mol\right)\)
\(\Rightarrow V_{H_2}=0,1.22,4=2,24\left(l\right)\)
Bạn tham khảo nhé!

a)
\(Zn+H2SO4\rightarrow ZnSO4+H2\)
\(2Al+3H2SO4\rightarrow Al2\left(SO4\right)3+3H2\)
\(Fe+H2SO4\rightarrow FeSO4+H2\)
b) giải sử khối KL cùng là \(m\left(g\right)\)
\(\Rightarrow n_{Zn}=\frac{m}{65}\Rightarrow n_{H_2}=\frac{m}{65}\)
\(\Rightarrow n_{Al}=\frac{m}{27}\Rightarrow n_{H_2}=1,5.\frac{m}{27}\)
\(\Rightarrow n_{Fe}=\frac{m}{56}\Rightarrow n_{H_2}=\frac{m}{56}\)
\(\Rightarrow Al\)
c) Giả sử : \(n_{H_2}=0,15mol\)
\(\Rightarrow n_{Zn}=0,15mol\Rightarrow m=9,75g\)
\(\Rightarrow n_{Al}=0,1mol\Rightarrow m=2,7g\)
\(\Rightarrow n_{Fe}=0,15mol\Rightarrow m=8,4g\)
\(\Rightarrow Al\)

\(n_{H_2}=\dfrac{5,6}{22,4}=0,25(mol)\\ a,PTHH:Fe+2HCl\to FeCl_2+H_2\\ 2Al+6HCl\to 2AlCl_3+3H_2\)
\(b,\) Đặt \(n_{Fe}=x(mol);n_{Al}=y(mol)\)
\(\Rightarrow 56x+27y=8,3(1)\)
Theo PTHH: \(x+1,5y=0,25(2)\)
\((1)(2)\Rightarrow x=y=0,1(mol)\\ \Rightarrow \%_{Fe}=\dfrac{0,1.56}{8,3}.100\%=67,47\%\\ \%_{Al}=100\%-67,47\%=32,53\%\)

a) PTHH: \(Zn+2HCl\rightarrow ZnCl_2+H_2\uparrow\)
b+c) Áp dụng Định luật bảo toàn khối lượng:
\(m_{Zn}+m_{HCl}=m_{ZnCl_2}+m_{H_2}\)
\(\Rightarrow m_{ZnCl_2}=m_{Zn}+m_{HCl}-m_{H_2}=6,5+7,3-1=12,8\left(g\right)\)
Có 3 lọ mất nhãn đựng 3 dung dịch không màu NaCl H2SO4 K2SO4 trình bày phương pháp hóa học để nhận ra các chất trên. Viết phương trình phản ứng.

\(n_{Al} = \dfrac{2,7}{27} = 0,1(mol)\\ 2Al + 3H_2SO_4 \to Al_2(SO_4)_3 + 3H_2\\ n_{H_2} = \dfrac{3}{2}n_{Al} = 0,15(mol)\\ \Rightarrow V_{H_2} = 0,15.22,4 = 3,36(lít)\\ n_{HCl} = \dfrac{8,1}{36,5} = \dfrac{81}{365}(mol)\\ 2Al + 6HCl \to 2AlCl_3 + 3H_2\\ \dfrac{n_{Al}}{2} = 0,05 > \dfrac{n_{HCl}}{6} = \dfrac{27}{730} \to Al\ dư\\ n_{Al\ pư} = \dfrac{1}{3}n_{HCl} = \dfrac{27}{365}(mol)\\ \)
\(m_{Al\ dư} = 2,7 - \dfrac{27}{265}.27 = 0,703(gam)\)
