Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) đây nha : https://hoc24.vn/hoi-dap/question/637285.html
câu 2 cũng chả khác gì cả

TenAnh1
TenAnh1
A = (-4, -6.26)
A = (-4, -6.26)
A = (-4, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
Do \(\overrightarrow{NP}=\overrightarrow{DC}\); \(\overrightarrow{AM}=\overrightarrow{BA}\Rightarrow\overrightarrow{MA}=\overrightarrow{AB}\).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
Vì vậy \(\overrightarrow{NP}=\overrightarrow{MA}\) nên tứ giác NPAM là hình bình hành.
Vì vậy \(\overrightarrow{PA}=\overrightarrow{NM}\). (1)
Mà \(\overrightarrow{MN}=\overrightarrow{DA}\) suy ra \(\overrightarrow{NM}=\overrightarrow{AD}\) . (2)
Mặt khác \(\overrightarrow{AD}=\overrightarrow{BC}\) (do tứ giác ABCD là hình bình hành). (3)
Từ (1);(2);(3) suy ra:\(\overrightarrow{PA}=\overrightarrow{BC}\).
Mà \(\overrightarrow{PQ}=\overrightarrow{BC}\Rightarrow\overrightarrow{PQ}=\overrightarrow{PA}\).
Vì vậy hai điểm A và Q trùng nhau nên \(\overrightarrow{AQ}=\overrightarrow{0}\).

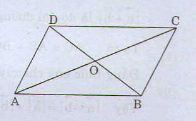
1)\(VT=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{CO}+\overrightarrow{DO}+\overrightarrow{OC}+\overrightarrow{OC}=\overrightarrow{CO}+\overrightarrow{OC}+\overrightarrow{DO}+\overrightarrow{OD}=\overrightarrow{0}\)
2)\(VT=\overrightarrow{DA}-\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\)
3)\(VT=\overrightarrow{DO}+\overrightarrow{AO}=\overrightarrow{OB}+\overrightarrow{AO}=\overrightarrow{AB}\)
4)\(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}=\overrightarrow{MB}+\overrightarrow{MD}\left(đpcm\right)=\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OD}=2\overrightarrow{MO}\left(đpcm\right)\)
Chúc bạn học tốt!!!!!
Đăng kí kênh Youtube 'Ban Mai Anime' giúp mình nhé!!!!

TenAnh1
TenAnh1
A = (-4.34, -5.84)
A = (-4.34, -5.84)
A = (-4.34, -5.84)
B = (11.02, -5.84)
B = (11.02, -5.84)
B = (11.02, -5.84)
Hình thoi nhận O là tâm đối xứng.
\(\left|x_A\right|=\left|x_C\right|=2AC\)\(\Rightarrow\left|x_A\right|=\left|x_C\right|=8:2=4\).
Do \(\overrightarrow{OC}\) và \(\overrightarrow{i}\) cùng hướng nên \(x_C=4;x_A=-4\).
A, C nằm trên trục hoành nên \(y_A=y_C=0\).
Vậy \(A\left(-4;0\right);C\left(4;0\right)\).
\(\left|y_B\right|=\left|y_D\right|=2BD\)\(\Rightarrow\left|y_B\right|=\left|y_D\right|=6:2=3\).
Do \(\overrightarrow{OB}\) và \(\overrightarrow{j}\) cùng hướng nên \(y_B=3;y_D=-3\).
B, D nằm trên trục tung nên \(x_B=x_D=0\).
Vậy \(B\left(0;3\right);D\left(0;-3\right)\).
b) \(x_I=\dfrac{x_B+x_C}{2}=\dfrac{0+4}{2}=2\); \(y_I=\dfrac{y_B+y_C}{2}=\dfrac{3+0}{2}=\dfrac{3}{2}\).
Vậy \(I\left(2;\dfrac{3}{2}\right)\).
\(x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{-4+0+4}{3}=0\).
\(y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{0+3+0}{3}=1\).
Vậy \(G\left(0;1\right)\).
c) I' đối xứng với I qua tâm O nên \(I'\left(-2;-\dfrac{3}{2}\right)\).
d) \(\overrightarrow{AC}\left(8;0\right);\overrightarrow{BD}\left(0;-6\right);\overrightarrow{BC}\left(4;-3\right)\).

1.D \(\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{BC}\right)=\dfrac{1}{3}\left(2\overrightarrow{BM}\right)=\dfrac{2}{3}\overrightarrow{BM}=\overrightarrow{BG}\)
2.A \(\overrightarrow{DA}+\overrightarrow{DB}+2.\overrightarrow{DC}=2.\overrightarrow{DM}+2.\overrightarrow{DC}=0\)
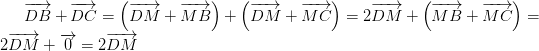
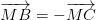
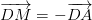
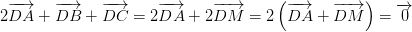
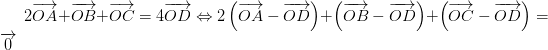
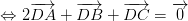 luôn đúng theo câu a
luôn đúng theo câu a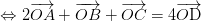 , với O là điểm tùy ý
, với O là điểm tùy ý
Bài 2:
a: \(\overrightarrow{AC}-\overrightarrow{BC}=\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{CB}+\overrightarrow{AC}=\overrightarrow{DC}\)
=>vecto AB=vecto DC
=>ABCD là hình bình hành
b: \(\Leftrightarrow\overrightarrow{DB}-\overrightarrow{DA}=2\cdot\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{AD}+\overrightarrow{DB}=2\cdot\overrightarrow{DC}\)
=>vecto AB=2 vecto DC
=>ABCD là hình thang