Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m 2 ), điều kiện x ≥ 0, y ≥ 0, ta có x + y ≤ 0
Số công cần dùng là 20x + 30y ≤ 180 hay 20 + 3y ≤ 18
Số tiền thu được là
F = 3000000x + 4000000y (đồng)
Hay F = 3x + 4y (đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình
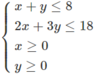
Sao cho F = 3x + 4y đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0;6), B(6;2), C(8;0) và O(0;0).
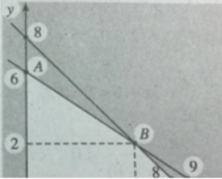
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra x = 6, y = 2 (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6a đậu, 2a cà, thu hoạch 26 000 000 đồng.

Gọi diện tích trồng đậu là x ( đơn vị là a, 0 < x < 8).
Diện tích trồng cà là: 8 - x (a).
Tổng số tiền thu được là: \(3000000x+4000000\left(8-x\right)=32000000-1000000x\).
Tổng số công cần là: \(20x+30\left(8-x\right)=240-10x\).
Theo yêu cầu của đề bài: \(240-10x\le180\)\(\Leftrightarrow10x\ge60\)\(\Leftrightarrow x\ge6\).
Mặt khác \(x\le8\) nên \(6\le x\le8\).
Ta cần \(32000000-1000000x\) đạt giá trị lớn nhất nên \(x=6\).
Vậy diện tích trồng đậu 6a, diện tích trồng cà là 2a thì số tiền thu được lớn nhất bằng: \(32000000-1000000.6=26000000\) đồng.

a)
Để quy hoạch x sào đất trồng cà tím, cần \(200\,000.x\)(đồng)
Để quy hoạch y sào đất trồng cà chua, cần \(100\,000.y\)(đồng)
Tổng số tiền để mua hạt giống là \(200{\rm{ }}000.x + 100{\rm{ }}000.y\) (đồng), tối đa là 9 triệu đồng nên ta có bất phương trình: \(0,2x + 0,1y \le 9\)
Ngoài ra số sào đất là số không âm nên \(x \ge 0\) và \(y \ge 0\)
b) + Cặp số (20; 40) thỏa mãn cả 3 bất phương trình trên vì \(0,2.20 + 0,1.40 = 8 < 9\).
+ Cặp số (40; 20) không thỏa mãn các bất phương trình trên vì \(0,2.40 + 0,1.20 = 10 > 9\).
+ Cặp số (-30; 10) không thỏa mãn các bất phương trình trên vì \( - 30 < 0\).

a) Số tiền cô Lan thu được nếu bán vào thời điểm 27-7-2020 là:
\(86\;000\;.\;5\;000 = 430\;000\;000\)(đồng)
Số tiền cô Lan thu được nếu bán vào thời điểm 30-12-2020 là:
\(108\;800\;.\;5\;000 = 544\;000\;000\)(đồng)
Số tiền cô Lan thu được nếu bán vào thời điểm 10-5-2021 là:
\(91\;000\;.\;5\;000 = 455\;000\;000\)(đồng)
b) Lãi suất 6%/năm cho kì hạn một tháng, tương ứng là 6:12=0,5(%)/ tháng
Vậy số tiền cô Lan nhận được sau 11 tháng là:
\(T = 511\;000\;000.{(1 + 0,5\% )^{11}} \approx 539\;818\;271\)(đồng)
TRAO ĐỔI
a) Với tình huống như trên cô Lan nên đầu tư ở thời điểm 27-7-2020 và bán ra vào thời điểm 30-12-2020.
b)
+) Nếu cô Lan gửi tiết kiệm, đến ngày 10-5-2021, số tiền thu được là: \(539\;818\;271\)(đồng)
+) Nếu cô Lan đầu tư, thì đến ngày 10-5-2021, số tiền thu được là: \(455\;000\;000\)(đồng)
=> Như vậy cô Lan nên chọn hình thức tiết kiệm.

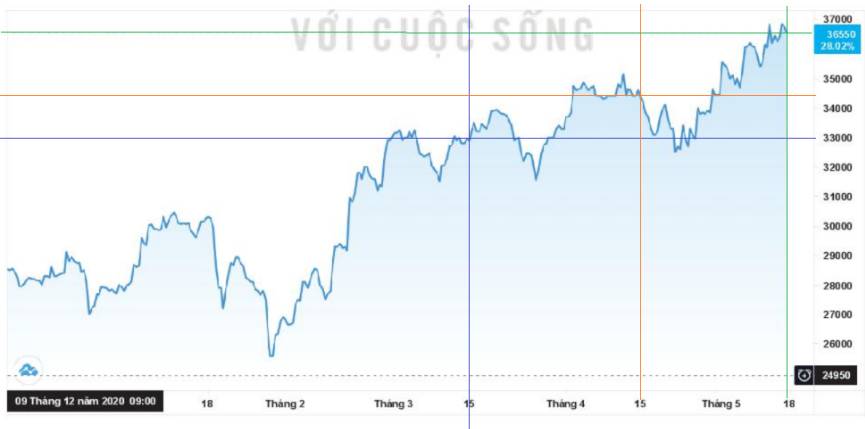
Số cổ phiếu mà anh Tiến mua được là: \(898\;200\;000:24\;950 = 36\;000\) (cổ phiếu)
a) Vào thời điểm 15-3-2021, giá mỗi cổ phiếu là 33 000 (đồng)
Số tiền thu được nếu bán vào thời điểm này là: \(36\;000\;.\;33\;000 = 1\;188\;000\;000\)(đồng)
b) Vào thời điểm 15-4-2021, giá mỗi cổ phiếu là 34 400 (đồng)
Số tiền thu được nếu bán vào thời điểm này là: \(36\;000\;.\;34\;400 = 1\;238\;400\;000\)(đồng)
c) Vào thời điểm 18-5-2021, giá mỗi cổ phiếu là 36 550 (đồng)
Số tiền thu được nếu bán vào thời điểm này là: \(36\;000\;.\;36\;550 = 1\;315\;800\;000\)(đồng)