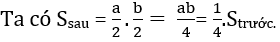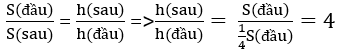Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng thể tích bể nước là :
4 x 2,5 x 1,8= 18 (m3)
Chiều cao bể nước sau khi thay đổi là :
18 : 4 : 3 = 1,5 ( m )
Thể tích của bể nước là:
\(\left(4\times2,5\right)\times1,8=18\left(m^3\right)\)
Chiều cao của bể nước là:
\(18\div\left(4\times3\right)=1,5\left(m\right)\)
Vậy chiều cao của bể nước là \(1,5\) \(m\) .

Thể tích hình hộp chữ nhật V = S.h
Vì thể tích không đổi nên S và h là hai đại lượng tỉ lệ nghịch.
Diện tích đáy giảm: 1,5. 1,5 = 2,25 (lần)
Khi đó chiều cao h tăng thêm 2,25 lần.

* Thể tích hình hộp chữ nhật V = S.h
Trong đó; S là diện tích đáy và h là chiều cao của hình hộp chữ nhật.
* Gọi chiều dài, chiều rộng và chiều cao của bể nước theo dự định ban đầu lần lượt là a, b và h (a, b, h > 0).
Khi giảm cả chiều dài và chiều rộng đáy bể đi 1,5 lần ta được chiều dài và chiều rộng mới là: 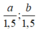
* Diện tích đáy bể theo dự định ban đầu là: S = ab.
Diện tích đáy bể sau khi thay đổi kích thước là: 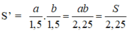
* Vì thể tích không đổi nên diện tích đáy bể và chiều cao là hai đaị lượng tỉ lệ nghịch nên ta có: S.h = S’.h’
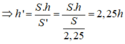
Vậy để thể tích bể không đổi thì chiều cao bể tăng gấp 2,25 lần so với dự định


Vì V = h.S => diện tích đáy chiều cao ( khi V không đổi ) tỉ lệ nghịch với nhau .
Gọi a,b là chiều rộng và chiều dài ban đầu thì a/2,b/2 là chiều rộng và chiều dài lúc sau
Ta có
S2 =a/2 × b/2 = a×b/2= 1/4 =s1
Theo tính chất của đại lượng tỉ lệ nghịch ta có
S1/s2= h2/h1 => h2/h1 = s1/1/4s1
=> h2/h1 =4 => h2 = 4h1

Hướng dẫn:
Gọi A và B là hai điểm dân cư, C là điểm đặt trạm y tế.

Vì C cách đều AB nên C thuộc đường trung trực của AB mà C ∈ xy nên C là giao điểm của xy và đường trung trực của AB
Vì V = hS ⇒ diện tích đáy và chiều cao (khi V không đổi) tỉ lệ nghịch với nhau.
Gọi a,b là chiều rộng và chiều dài ban đầu thì 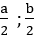
Theo tính chất của đại lượng tỉ lệ nghịch ta có
Vậy chiều cao lúc sau của bể phải tăng lên 4 lần.

Vì V = hS ⇒ diện tích đáy và chiều cao (khi V không đổi) tỉ lệ nghịch với nhau.
Gọi a,b là chiều rộng và chiều dài ban đầu thì 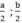 là chiều rộng và chiều dài lúc sau. Ta có:
là chiều rộng và chiều dài lúc sau. Ta có:
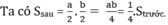
Theo tính chất của đại lượng tỉ lệ nghịch ta có
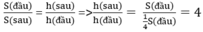
Vậy chiều cao lúc sau của bể phải tăng lên 4 lần.