Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
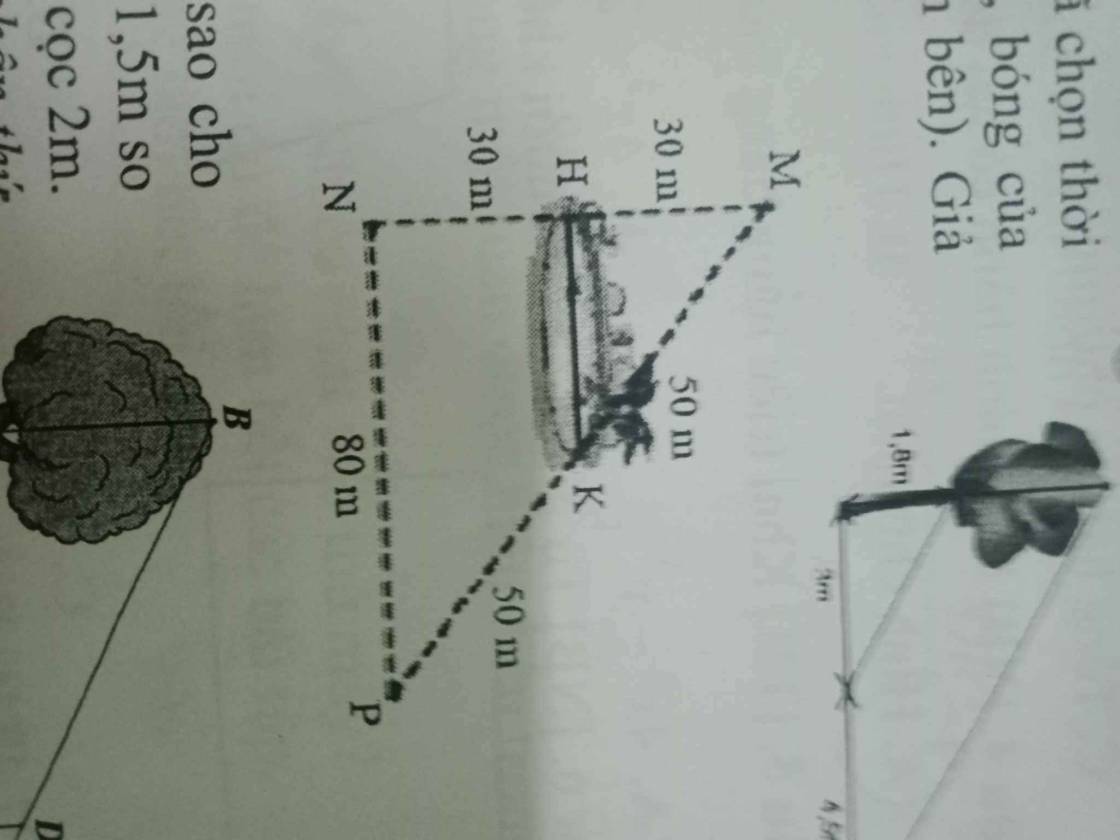
MN = MH + HN = 30 + 30 = 60 (m)
MP = MK + KP = 50 + 50 = 100
Lại có:
MH/MN = 30/60 = 1/2
MK/MP = 50/100 = 1/2
⇒ MH/MN = MK/MP = 1/2
⇒ HK // MN
⇒ HK/NP = MH/MN = 1/2
⇒ HK = NP : 2
= 80 : 2
= 40 (m)

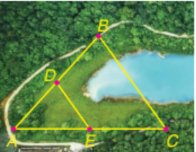
Xét ΔCAB có FE//AB
nên \(\dfrac{CF}{FA}=\dfrac{CE}{EB}\)
=>\(\dfrac{30}{EB}=\dfrac{20}{40}=\dfrac{1}{2}\)
=>\(EB=30\cdot2=60\left(m\right)\)

Theo đề bài, ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF, áp dụng định lí Thalès, ta có:
\(\dfrac{{EC}}{{BE}} = \dfrac{{CF}}{{AF}}\) hay \(\dfrac{{30}}{{BE}} = \dfrac{{20}}{{40}}\)
Suy ra \(BE = \dfrac{{30.40}}{{20}} = 60\) (m).
Vậy khoảng cách giữa hai vị trí B và E bằng 60 m.

Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.
Suy ra DE là đường trung bình của tam giác ABC.
Do đó \(DE = \frac{1}{2}BC\) suy ra BC = 2DE = 2 . 500 = 1 000 (m)
Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.

Giải VNEN toán 8 bài 2: Đường trung bình của tam giác
Người đăng: Mai Anh - Ngày: 20/03/2019Giải bài 2: Đường trung bình của tam giác - Sách VNEN toán 8 tập 1 trang 66. Phần dưới sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu. Hi vọng các em học sinh nắm tốt kiến thức bài học.
A. Hoạt động khởi động
Thực hiện đo đạc
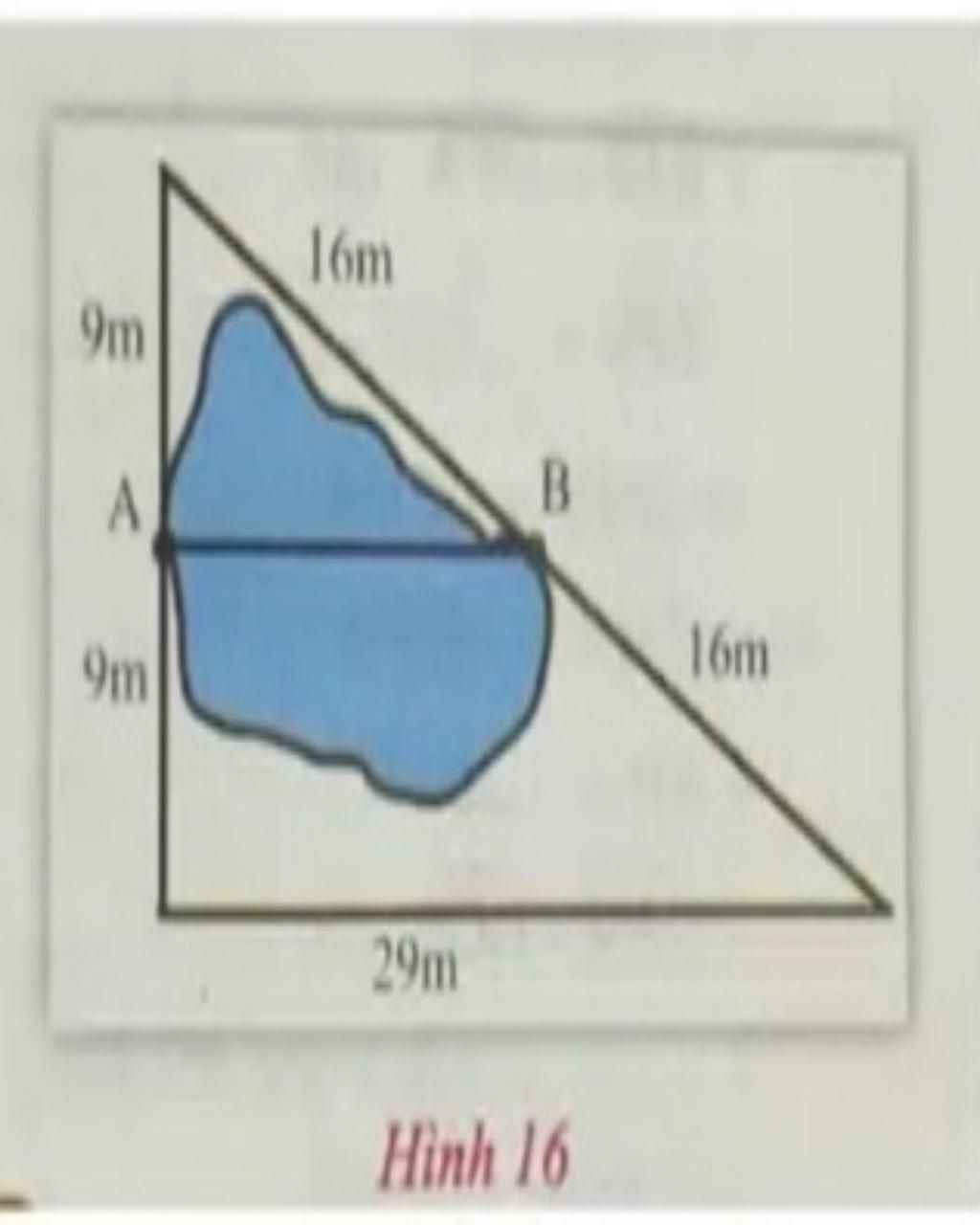
Bác Ba muốn tính khoảng cách giữa hai vị trí ở hai bên bờ ao cá. Để làm điều đó bác đã thực hiện đo đạc và vẽ mô phỏng theo tỉ lệ 1 : 600 như hình 16.
Em hãy giúp bác Ba tính khoảng cách giữa hai vị trí A và B ở hai bên bờ ao cá nhé!

Trả lời:

Vẽ điểm F sao cho B là trung điểm của AF.
Dễ dàng nhận thấy: ΔAOB = ΔFNB (c.g.c) ⇒ AO = FN và Oˆ = Nˆ.
Ta có: OA = AM (gt) và OA = FN ⇒ AM = FN.
Lại có Oˆ = Nˆ mà hai góc này ở vị trí so le trong nên AO // FN.
⇒ AM // FN ⇒ AMNF là hình thang.
Hình thang AMNF có hai đáy AM và FN bằng nhau nên hai cạnh bên AF và MN song song và bằng nhau.
⇒ AB // MN, AB = 12AF = 12MN.
Như vậy, độ dài đoạn AB sẽ bằng 14,5m.
Cái này mình chr gợi ý như vậy thôi bạn phỉa tự làm chi tiết ra nhé<3

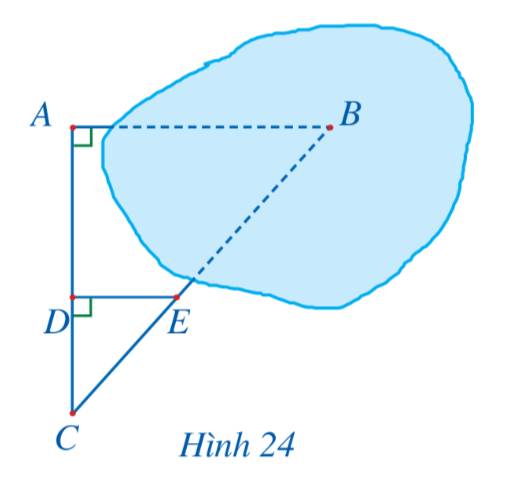
Ta có:
\(\left. \begin{array}{l}AB \bot AC\\DE \bot AC\end{array} \right\} \Rightarrow AB\parallel DE\)
Xét tam giác ABC với \(AB\parallel DE\) có:
\(\frac{{DE}}{{AB}} = \frac{{CD}}{{CA}}\) (Hệ quả của định lý Thales)
\(\begin{array}{l} \Rightarrow \frac{{18}}{{AB}} = \frac{{20}}{{50}}\\ \Rightarrow AB = 18.50:20\\ \Rightarrow AB = 45\end{array}\)
Vậy khoảng cách AB là 45m.

Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:
\(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{CE}}{{C{\rm{D}}}}\) hay \(\dfrac{{400}}{{300}} = \dfrac{{500}}{{C{\rm{D}}}}\)
Suy ra \(C{\rm{D}} = \dfrac{{300.500}}{{400}} = 375\) (m).
Vậy khoảng cách giữa C và D bằng 375 m

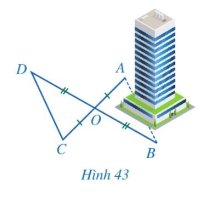
Ta có: AC giao với BD tại O.
Mà: OA = OC; OB = OD
Nên tứ giác ABCD là hình bình hành
Suy ra AB = CD = 100m.
 D.AB=32cm
D.AB=32cm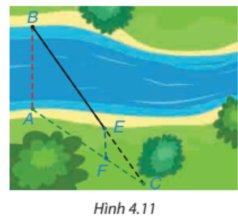

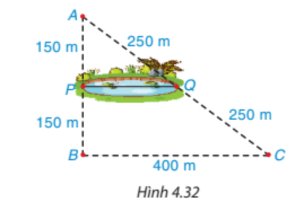
Áp dụng định lí Ta-lét trong tam giác ABC có PQ // BC, ta có:
\(\dfrac{PQ}{BC}=\dfrac{AP}{AB}=\dfrac{AP}{AP+PB}\\ \Leftrightarrow\dfrac{PQ}{400}=\dfrac{150}{150+150}\\ \Leftrightarrow PQ=200\left(m\right).\)