K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 9 2021
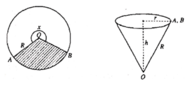
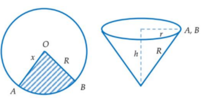
Gọi phần cung tròn bị cắt có góc ở tâm bằng x độ \(\left(0< x< 360\right)\)
Chu vi đường tròn ban đầu: \(2\pi R\)
Chu vi sau khi bị cắt: \(2\pi R\left(1-\dfrac{x}{360}\right)\)
(Và lưu ý chu vi này đúng bằng chu vi đường tròn đáy hình nón được tạo ra, đường sinh nón bằng R)
Gọi đáy nón có bán kính \(r\)
\(\Rightarrow2\pi r=2\pi R\left(1-\dfrac{x}{360}\right)\Rightarrow r=R\left(1-\dfrac{x}{360}\right)\)
\(\Rightarrow V_{nón}=\dfrac{1}{3}\pi r^2.\sqrt{R^2-r^2}=f\left(x\right)\)
Giờ chắc khảo sát hàm \(f\left(x\right)\) tìm x là được

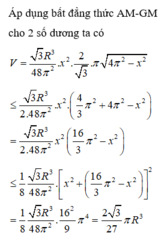
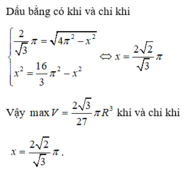
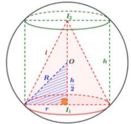

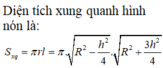
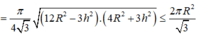



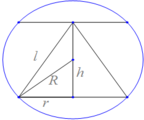
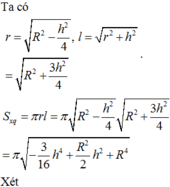
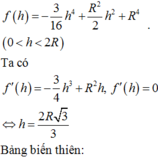
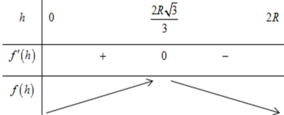
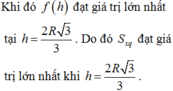
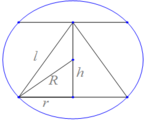
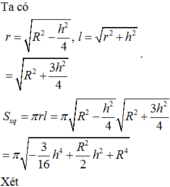
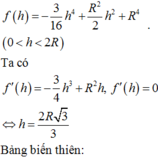
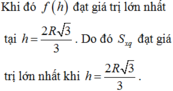

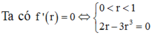

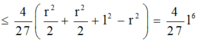
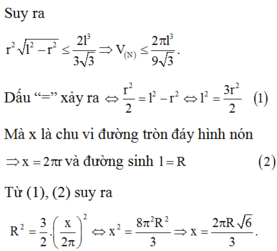

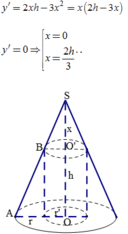
đặt chiều cao chóp = h
=> r đáy=\(\sqrt{4^2-h^2}\)
V = 1/3.h.(42-h2)\(\pi\)
đặt h.(4-h^2) là g(h)
=> bài toán trở thành tìm h ( 0<h<4) để g(h) max
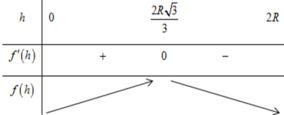
=> 2 cách: tính đạo hàm hoặc chạy mode 7
=> hàm max tại h=\(\frac{4\sqrt{3}}{3}\)
=> V max=\(\frac{128\sqrt{3}}{27}\pi\)
v