Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Gọi x; y lần lượt là số xe loại M, loại F cần thuê
Từ bài toán ta được hệ bất phương trình
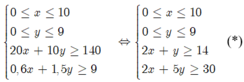
Tổng chi phí T(x; y) = 4x+ 3y (triệu đồng)
Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T( ;xy) nhỏ nhất.
Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.

Sau khi mua thì Cường còn lại \(\frac{3}{5}=\frac{15}{25}\) số tiền, Huy còn lại \(\frac{5}{7}=\frac{15}{21}\) số tiền.
Ta thấy thấy tiền của Cường có 25 phần thì tiền của Huy có 21 phần.
Giá trị 1 phần là:
219000:(15+15)=7300 (đồng)
Tiền của Cường có được là:
7300x25=182500(đồng)
Tiền của Huy có được là:
7300x21=153300 (đồng)
Đáp số:153300 đồng

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là L = 3x + 5y (nghìn đồng).
Theo đề bài: Nhóm A cần 2x + 2y máy;
Nhóm B cần 0x + 2y máy;
Nhóm C cần 2x + 4y máy;
Vì số máy tối đa ở nhóm A là 10 máy, nhóm B là 4 máy, nhóm C là 12 máy nên x, y phải thỏa mãn hệ bất phương trình: 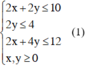
Khi đó bài toán trở thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm (x = xo; y = yo) nào cho L = 3x + 5y lớn nhất.
Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE kể cả miền trong.
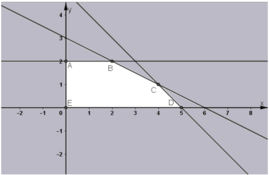
Ta có: L đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác ABCDE.
Tính giá trị của biểu thức L = 3x + 5y tại các đỉnh ta được:
Tại đỉnh A(0;2), L = 10
Tại đỉnh B(2; 2), L = 16
Tại đỉnh C(4; 1), L = 17
Tại đỉnh D(5; 0), L = 15
Tại đỉnh E(0; 0), L = 0.
Do đó, L = 3x + 5y lớn nhất là 17 (nghìn đồng) khi: x = 4; y = 1
Vậy để có tiền lãi cao nhất, cần sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.

TRẢ LỜI:
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.
^^
Gọi số tiền của 3 người lần lượt là a, b và c.
Áp dụng tính chất của day tỉ số bằng nhau, ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{18}{9}=2\)
\(\frac{a}{2}=2\Rightarrow a=4\)
\(\frac{b}{3}=2\Rightarrow b=6\)
\(\frac{c}{4}=2\Rightarrow c=8\)
Vậy số tiền của 3 người lần lượt là 4 triệu, 6 triệu và 8 triệu.