Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tìm GTLN của \(\dfrac{1}{x^2+2010}\)
Để GTBT đạt lớn nhất \(\Leftrightarrow x^2+2010\) đạt giá trị nhỏ nhất.
Vì \(x^2\ge0\forall x\), \(2010\ge0\)
Vậy giá trị nhỏ nhất của \(x^2+2010=2010\Leftrightarrow x=0\)
\(\Rightarrow\) GTLN của biểu thức \(\dfrac{1}{x^2+2010}=\dfrac{1}{2010}\Leftrightarrow x^2=0\)
b) Xét dấu của hai biểu thức :
+) Biểu thức (1) : \(2a^3bc\)
+) Biểu thức (2) : \(-3a^5b^3c^2\)
Ta nhận thấy rằng ở (1), số mũ của a là số mũ lẻ ; ở (2) thì số mũ của a là số mũ lẻ => a ở biểu thức (1) và a ở biểu thức (2) cùng dấu.
Ta lại thấy rằng ở (1), số mũ của b là số mũ lẻ và ở (2) cũng là số mũ lẻ => b ở biểu thức (1) và (2) cùng dấu.
Lại có, biểu thức (1) có số 2 là số nguyên dương, biểu thức (2) có số -3 là số nguyên âm => trái dấu.
Vậy c mang dấu dương (+) thì biểu thức \(2a^3bc\) trái dấu với biểu thức \(-3a^5b^3c^2\)
a) \(x^2\ge0\Rightarrow x^2+2010\ge2010\Rightarrow\dfrac{1}{x^2+2010}\le\dfrac{1}{2010}\)
=> \(\dfrac{1}{x^2+2010}\) đạt giá trị lớn nhất là \(\dfrac{1}{2010}\) khi x2=0 <=> x=0
b) c có dấu âm
-----
bạn ơi cho mình hỏi câu hỏi này là vio vòng mấy đấy?

a: Để hai đơn thức cùng dấu thì \(-2a^5b^2\cdot3a^4b^6>0\)
\(\Leftrightarrow a^9b^8< 0\)
=>a<0
b: Vì hai đơn thức trái dấu nên \(12a^8b^4c^3>0\)
=>c>0

2a3bc trai dau voi -3a5b3c2
=>2a3bc.(-3a5b3c2)<0
=> -6a8b4c<0
mà -6a8b4<0
=>c3>0=>C>0
2a3bc trai dau voi -3a5b3c2
=>2a3bc.(-3a5b3c2)<0
=> -6a8b4c<0
mà -6a8b4<0
=>c3>0=>C>0
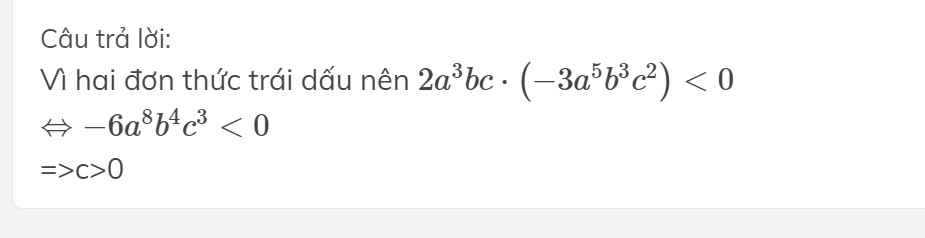
Lời giải:
Giả sử 3 đơn thức trên đều cùng nhận giá trị âm
Khi đó:
\(\frac{1}{2}a^2bc^3.\frac{-1}{3}a^3b^5c.\frac{-5}{3}a^5b^2c^2=\text{số âm}.\text{số âm}.\text{số âm}\)
\(=\text{số dương}.\text{số âm}=\text{số âm}\)
Hay: \(\frac{5}{18}a^{2+3+5}b^{1+5+2}c^{3+1+2}=\text{số âm}\)
\(\Leftrightarrow \frac{5}{18}a^{10}b^8c^6=\text{số âm}(*)\)
Do số mũ của $a,b,c$ đều là số chẵn nên \(a^{10}, b^8, c^6\geq 0; \frac{5}{18}>0\Rightarrow \frac{5}{18}a^{10}b^{8}c^6\geq 0\)
Do đó $(*)$ sai. Vậy ba đơn thức trên không thể có cùng giá trị âm.