Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số máy cày của 3 đọi lần lượt là: a;b;c (máy)
Với cùng 1 diện tích đất thì số máy cày và thời gian làm xong việc là 2 ĐLTLN; ta có:
a3=b5=c6=>a/(1/3)=b/(1/5)=c/(1/6) và b-c=1
ttcdtsbn; ta có:
a/(1/3)=b/(1/5)=c/(1/6)=(b-c)/(1/5-1/6)=1/(1/30)=30
Khi đó: a=10; b=6; c=5
Vậy số máy của 3 đội lần lượt là 10;6;5
Gọi số máy cày của 3 đọi lần lượt là: a;b;c (máy)
Với cùng 1 diện tích đất thì số máy cày và thời gian làm xong việc là 2 ĐLTLN; ta có:
a3=b5=c6=>a/(1/3)=b/(1/5)=c/(1/6) và b-c=1
ttcdtsbn; ta có:
a/(1/3)=b/(1/5)=c/(1/6)=(b-c)/(1/5-1/6)=1/(1/30)=30
Khi đó: a=10; b=6; c=5
Vậy số máy của 3 đội lần lượt là 10;6;5

Gọi a,b,c là số máy cày của mỗi đội
Vì số máy và số ngày tỉ lệ nghịch với nhau
nên ta có: a,b,c TLN với 3,5,6
=> a3 = b5 = c6
=> \(\frac{\frac{a}{1}}{3}\)=\(\frac{\frac{b}{1}}{5}\)=\(\frac{\frac{c}{1}}{6}\) và b-c = 1
Áp dụng tính chất dãy tỉ số bằng nhau
Ta có: \(\frac{\frac{a}{1}}{3}\)=\(\frac{\frac{b}{1}}{5}\)=\(\frac{\frac{c}{1}}{6}\)=\(\frac{b-c}{\frac{1}{5}-\frac{1}{6}}\)=\(\frac{\frac{1}{1}}{30}\)=30
\(\frac{\frac{a}{1}}{3}\)=30 => a = 10
\(\frac{\frac{b}{1}}{5}\)=30 => b = 6
\(\frac{\frac{c}{1}}{6}\)=30 => c = 5
Vậy số máy của mỗi đội lần lượt là 10 máy, 6 máy, 5 máy
Gọi \(a,b,c\) lần lượt là số máy cày của đội \(I,II,III\)
Theo đề , ta có : \(b-c=1\)
Do số máy cày và số ngày tỉ lệ nghịch với nhau nên ta có :
\(3a=5b=6c\)
\(\Rightarrow\frac{3a}{30}=\frac{5b}{30}=\frac{6c}{30}\)
\(\Rightarrow\frac{a}{10}=\frac{b}{6}=\frac{c}{5}\) và \(b-c=1\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{10}=\frac{b}{6}=\frac{c}{5}=\frac{b-c}{6-5}=\frac{1}{1}=1\)
\(\Rightarrow a=10;b=6;c=5\)
Vậy số máy cày của đội \(I,II,III\) lần lượt là \(10\) máy ; \(6\) máy ; \(5\) máy

Gọi số máy cày của ba đội lần lượt là x, y, z (máy)
Vì diện tích cày là như nhau nên số máy cày và thời gian là hai đại lượng tỉ lệ nghịch
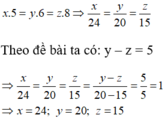
Chọn đáp án A

Gọi x (máy), y (máy), z (máy) lần lượt là số máy cày của đội một, đội hai, đội ba (x, y, z N*)
Do các máy cùng năng suất và cùng cày ba cánh đồng cùng diện tích nên số máy cày và số ngày hoàn thành là hai đại lượng tỉ lệ nghịch
⇒ 3x = 5y = 6z
⇒ x/(1/3) = y/(1/5) = z/(1/6)
Do đội thứ ba ít hơn đội thứ hai 1 máy nên: y - z = 1
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/(1/3) = y/(1/5) = z/(1/6) = (y - z)/(1/5 - 1/6) = 1/(1/30) = 30
x/(1/3) = 30 ⇒ x = 30 . 1/3 = 10 (nhận)
y/(1/5) = 30 ⇒ y = 30 . 1/5 = 6 (nhận)
z/(1/6) = 30 ⇒ z = 30 . 1/6 = 5 (nhận)
Vậy số máy cày của đội một, đội hai, đội ba lần lượt là 10 máy, 6 máy, 5 máy

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{5}=\dfrac{b-c}{6-5}=1\)
Do đó: a=10; b=6; c=5

Gọi số máy của đội 1;2;3 lần lượt là a,b,c
Theo đề, ta có: 3a=5b=6c và a-c=5
=>a/10=b/6=c/5 và a-c=5
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{5}=\dfrac{a-c}{10-5}=1\)
=>a=10; b=6; c=5

Gọi x (máy), y (máy), z (máy) lần lượt là số máy cày của các đội 1, 2, 3 (điều kiện x, y, z ∈ N*)
Vì diện tích các cánh đồng là như nhau nên số máy cày và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch, suy ra 3x = 5y = 6z.
Đội thứ hai nhiều hơn đội thứ ba 1 máy nên y – z = 1.
Từ 3x = 5y = 6z, suy ra
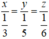
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
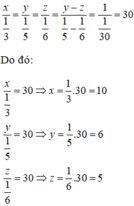
Vậy đội 1 có 10 máy cày, đội hai có 6 máy và đội 3 có 5 máy
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{3}}=\dfrac{b}{\dfrac{1}{5}}=\dfrac{c}{\dfrac{1}{6}}=\dfrac{a-b}{\dfrac{1}{3}-\dfrac{1}{5}}=\dfrac{4}{\dfrac{2}{15}}=30\)
Do đó: a=10; b=6; c=5