Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi vật I qua VTCB thì nó có vận tốc là: \(v=\omega.A\)
Khi thả nhẹ vật II lên trên vật I thì động lượng được bảo toàn
\(\Rightarrow M.v = (M+m)v'\Rightarrow v'=\dfrac{3}{4}v\)
Mà \(v'=\omega'.A'\)
\(\dfrac{v'}{v}=\dfrac{\omega'}{\omega}.\dfrac{A'}{A}=\sqrt{\dfrac{M}{\dfrac{4}{3}M}}.\dfrac{A'}{A}=\dfrac{3}{4}\)
\(\Rightarrow \dfrac{A'}{A}=\dfrac{\sqrt 3}{2}\)
\(\Rightarrow A'=5\sqrt 3cm\)
Chọn A.
Vận tốc của M khi qua VTCB: v = ωA = 10.5 = 50cm/s
Vận tốc của hai vật sau khi m dính vào M: v’ = Mv/(M+v)= 40cm/s
Cơ năng của hệ khi m dính vào M: W = 1/2KA'2= 1/2(m+M)v'2
A’ = 2căn5

Đáp án B
Hướng dẫn:
Tần số góc của dao động ω = k m = 10 rad/s
+ Dưới tác dụng của điện trường, vị trí cân bằng mới O′ của vật dịch chuyển về phía chiều dương cách vị trí cân bằng cũ O một đoạn Δ l 0 = q E k = 20.10 − 6 .10 4 10 = 2 cm.
Tại vị trí xuất hiện điện trường, ta có x ' = − Δ l 0 = − 2 cm, v ' = 20 3 cm/s.
→ Biên độ dao động của vật sau khi xuất hiện điện trường A ' = x ' 2 + v ' ω 2 = − 2 2 + 20 3 10 2 = 4 cm
Cơ năng của dao động E = 0 , 5 k A 2 = 8 m J .

Đáp án C
Hướng dẫn:
Hai vật sẽ tách khỏi nhau khi chúng cùng đi qau vị trí cân bằng. Tần số góc của hệ dao động ω = k 2 m .
→ Tốc độ của vật m tại vị trí hai vật tách nhau v = v m a x = ω A = 8 ω .
+ Biến cố xảy ra chỉ làm thay đổi tần số góc của hệ dao động mà không làm thay đổi vị trí cân bằng của hệ.
→ Tần số góc của hệ dao động lúc sau ω = k m = 2 ω .
→ Biên độ dao động mưới của vật m là A = v m a x ω ' = 8 ω ω ' = 4 2 cm.
+ Năng lượng của hệ E = 0 , 5 k A ' 2 = 16 m J .

\(f=\frac{1}{2\pi}\sqrt{\frac{g}{\Delta l}}=\frac{1}{2\pi}\sqrt{\frac{\pi^2}{0.16}}=1.25Hz\)

Chọn đáp án D
Giả sử chúng gặp nhau ở li độ x 1 , con lắc 1 đi về bên trái và con lắc 2 đi về bên phải. Sau một nửa chu kì thì chúng lại gặp nhau ở độ - x 1 , tiếp theo nửa chu kì gặp nhau ở li độ + x 1 . Như vậy, khoảng thời gian 2 lần gặp nhau liên tiếp là 2 - 1 T 2 = π m k = 0 , 01 s

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

Hướng dẫn:
Tần số góc của dao động ω = k m = 100 0 , 1 = 10 π rad/s → T = 0,2 s
+ Ban đầu vật ở vị trí cân bằng, sau khoảng thời gian Δt = 0,75T = 0,15 s vật đến vị trí biên (lò xo bị nén cực đại) → Năng lượng của con lắc lúc này chỉ là thế năng đàn hồi của lò xo.
+ Giữ cố định điểm chính giữa của lò xo → một nửa thế năng bị mất đi → Năng lượng dao động lúc sau sẽ là:
E′ = 0,5E → 1 2 k ' A ' 2 = 0 , 5 1 2 k A 2
với k′ = 2k → A'= 0,5A.
ü Đáp án A
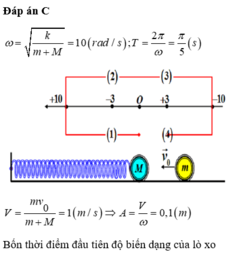

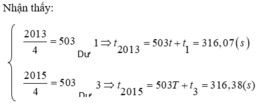

Đáp án C
Ta có ω 1 = ω 2 = ω 3 = 10 π rad / s
Phương trình dao động của vật 1 và vật 2 là:
x 1 = 3 cos ( 10 πt - π 2 ) c m x 2 = 1 , 5 cos ( 10 πt ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = ± A )
Trong quá trình dao động cả ba vật nằm trên một đường thẳng khi 2 x 2 = x 1 + x 3 ⇒ x 3 = 2 x 2 - x 1
tính chất trung bình
Bấm máy tính tổng hợp dao động ta được
Taị t = 0 và v 30 = - 30 π cm / s
Trường hợp x 2 = 1 , 5 cos ( 10 π t + π ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = - A )