
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



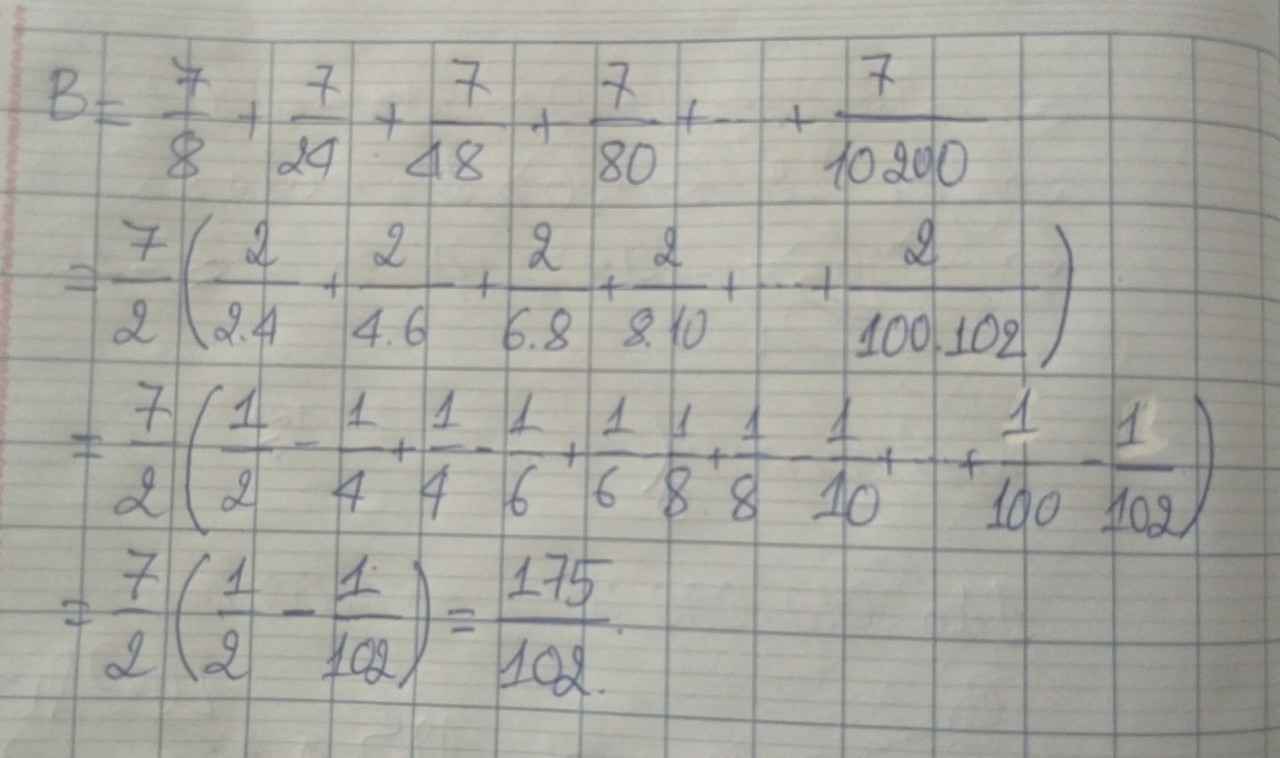
B = \(\frac{7}{2.4}+\frac{7}{4.6}+\frac{7}{6.8}+.....+\frac{7}{100.102}\)
ta có \(\frac{7}{2.4}=\frac{1}{2}\left(\frac{7}{2}-\frac{7}{4}\right);\frac{7}{4.6}=\frac{1}{2}\left(\frac{7}{4}-\frac{7}{8}\right);......;\frac{7}{100.102}=\frac{1}{2}\left(\frac{7}{100}-\frac{7}{102}\right)\)
⇒ B = \(\frac{1}{2}\left(\frac{7}{2}-\frac{7}{4}+\frac{7}{4}-\frac{7}{8}+....+\frac{7}{100}-\frac{7}{102}\right)\)
⇔ B = \(\frac{1}{2}\left(\frac{7}{2}-\frac{7}{102}\right)\)
⇔ B = \(\frac{1}{2}.\frac{175}{51}\)
⇔ B = \(\frac{175}{102}\)

\(\text{a) }\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\\ =\dfrac{3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)}{3}\\ =\dfrac{\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)}{3}\\ \\ =\dfrac{\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)}{3}\\ =\dfrac{\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)}{3}\\ =\dfrac{\left(2^{16}-1\right)\left(2^{16}+1\right)}{3}\\ =\dfrac{2^{32}-1}{3}\\ \)
\(\text{b) }24\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\\ =\left(5^2-1\right)\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\\ =\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right) \\ =\left(5^8-1\right)\left(5^8+1\right)\left(5^{16}+1\right)\\ =\left(5^{16}-1\right)\left(5^{16}+1\right)\\ =5^{32}-1\\ \)
\(\text{c) }48\left(7^2+1\right)\left(7^4+1\right)\left(7^8+1\right)\left(7^{16}+1\right)\\ =\left(7^2-1\right)\left(7^2+1\right)\left(7^4+1\right)\left(7^8+1\right)\left(7^{16}+1\right)\\ =\left(7^4-1\right)\left(7^4+1\right)\left(7^8+1\right)\left(7^{16}+1\right)\\ =\left(7^8-1\right)\left(7^8+1\right)\left(7^{16}+1\right)\\ =\left(7^{16}-1\right)\left(7^{16}+1\right)\\ =7^{32}-1\)

Ta có: \(7^{64}-48\left(7^2+1\right)\left(7^4+1\right)\left(7^8+1\right)\left(7^{16}+1\right)\left(7^{32}+1\right)\)
\(=7^{64}-\left(7^2-1\right)\left(7^2+1\right)\left(7^4+1\right)\left(7^8+1\right)\left(7^{16}+1\right)\left(7^{32}+1\right)\)
\(=7^{64}-\left(7^4-1\right)\left(7^4+1\right)\left(7^8+1\right)\left(7^{16}+1\right)\left(7^{32}+1\right)\)
\(=7^{64}-\left(7^{64}-1\right)\)
\(=7^{64}-7^{64}+1\)
\(=1.\)


P=24(7^2+1)(7^4+1)(7^8+1)(7^16+1)
=> 2P = 48(7^2+1)(7^4+1)(7^8+1)(7^16+1)
= (7^2 - 1)(7^2+1)(7^4+1)(7^8+1)(7^16+1)
= (7^4 - 1)(7^4+1)(7^8+1)(7^16+1)
= (7^8 - 1)(7^8+1)(7^16+1)
= (7^16 - 1)(7^16+1)
= 7^32 - 1
=> P = (7^32 - 1) / 2

\(\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{7+\sqrt{48}}}}\)
\(=\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{\left(2-\sqrt{3}\right)^2}}}\)
\(=\sqrt{5\sqrt{3}+5\sqrt{48-20+10\sqrt{3}}}\)
\(=\sqrt{5\sqrt{3}+5\sqrt{\left(5-\sqrt{3}\right)^2}}\)
\(=\sqrt{5\sqrt{3}+25-5\sqrt{3}}\)
= 5
\(\dfrac{\sqrt{3}-\sqrt{5+\sqrt{24}}+\sqrt{\sqrt{72}+11}}{\sqrt{6+\sqrt{20}}+\sqrt{2}-\sqrt{7+\sqrt{40}}}\)
\(=\dfrac{\sqrt{3}-\sqrt{\left(\sqrt{2}+\sqrt{3}\right)^2}+\sqrt{\left(3+\sqrt{2}\right)^2}}{\sqrt{\left(\sqrt{5}+1\right)^2}+\sqrt{2}-\sqrt{\left(\sqrt{2}+\sqrt{5}\right)^2}}\)
\(=\dfrac{\sqrt{3}-\sqrt{2}-\sqrt{3}+3+\sqrt{2}}{\sqrt{5}+1+\sqrt{2}-\sqrt{2}-\sqrt{5}}\)
\(=3\)

a.\(n^4+4=n^4+4n^2+4-4n^2=\left(n^2+2\right)^2-\left(2n\right)^2=\left(n^2+2n+2\right)\left(n^2-2n+2\right)\)
nguyên tố nên thừa số nhỏ hơn là \(n^2-2n+2=1\Leftrightarrow\left(n-1\right)^2=0\Leftrightarrow n=1\)thỏa mãn đề bài
b. ta có :\(n^{1994}+n^{1993}+1-\left(n^2+n+1\right)=\left(n^{1992}-1\right)\left(n^2+n\right)\)
mà \(1992⋮3\Rightarrow n^{1992}-1⋮n^3-1⋮n^2+n+1\)
nên \(n^{1994}+n^{1993}+1⋮n^2+n+1\)mà nó là số nguyên tố nên
\(n^2+n+1=1\Leftrightarrow n=0\) ( Do n là số tự nhiên nên n= -1 loại bỏ đi )

\(A=48\left(7^2+1\right)\left(7^4+1\right)...\left(7^{64}+1\right)\)
\(=\left(7^2-1\right)\left(7^2+1\right)\left(7^4+1\right)...\left(7^{64}+1\right)\)
\(=\left(7^4-1\right)\left(7^4+1\right)...\left(7^{64}+1\right)\)
\(=\left(7^8-1\right)\left(7^8+1\right)...\left(7^{64}+1\right)\)
\(...\)
\(=\left(7^{64}-1\right)\left(7^{64}+1\right)\)
\(=7^{128}-1\)