
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a)(2x^2-5x+3)(x^2-4x+3)=0`
`<=>[(2x^2-5x+3=0),(x^2-4x+3=0):}<=>[(x=3/2),(x=1),(x=3):}`
`=>A={3/2;1;3}`
`b)(x^2-10x+21)(x^3-x)=0`
`<=>[(x^2-10x+21=0),(x^3-x=0):}<=>[(x=7),(x=3),(x=0),(x=+-1):}`
`=>B={0;+-1;3;7}`
`c)(6x^2-7x+1)(x^2-5x+6)=0`
`<=>[(6x^2-7x+1=0),(x^2-5x+6=0):}<=>[(x=1),(x=1/6),(x=2),(x=3):}`
`=>C={1;1/6;2;3}`
`d)2x^2-5x+3=0<=>[(x=1),(x=3/2):}` Mà `x in Z`
`=>D={1}`
`e){(x+3 < 4+2x),(5x-3 < 4x-1):}<=>{(x > -1),(x < 2):}<=>-1 < x < 2`
Mà `x in N`
`=>E={0;1}`
`f)|x+2| <= 1<=>-1 <= x+2 <= 1<=>-3 <= x <= -1`
Mà `x in Z`
`=>F={-3;-2;-1}`
`g)x < 5` Mà `x in N`
`=>G={0;1;2;3;4}`
`h)x^2+x+3=0` (Vô nghiệm)
`=>H=\emptyset`.

\(A=\left\{x\in N|x^2-10x+21=0;x^3-x=0\right\}\\ x^2-10x+21=0\Leftrightarrow\left[{}\begin{matrix}x=7\\x=3\end{matrix}\right.\\ x^3-x=0\Leftrightarrow x\left(x-1\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\\ \Leftrightarrow A=\left\{-1;0;1;3;7\right\}\)
Xong r bạn liệt kê ra nha

Đáp án: B
2 x x 2 + 1 ≥ 1 ⇔ 2 x - x 2 - 1 x 2 + 1 ≥ 0 ⇔ 2 x - x 2 - 1 ≥ 0 ⇔ - ( x - 1 ) 2 ≥ 0 ⇔ x = 1 ⇒ A = { 1 } .
∆ ' = b 2 - 4 . Để phương trình vô nghiệm thì
∆ ' < 0 ⇔ b 2 - 4 < 0 ⇔ b 2 < 4 ⇔ - 2 < b < 2 ⇒ B = { - 1 ; 0 ; 1 } . ⇒ A ⊂ B .

b: \(\Leftrightarrow\left(x^2+3x+2\right)\left(x^2+3x-18\right)=-36\)
\(\Leftrightarrow\left(x^2+3x\right)^2-16\left(x^2+3x\right)=0\)
\(\Leftrightarrow\left(x^2+3x\right)\left(x^2+3x-16\right)=0\)
hay \(x\in\left\{0;-3;\dfrac{-3+\sqrt{73}}{2};\dfrac{-3-\sqrt{73}}{2}\right\}\)
c: \(\Leftrightarrow6x^4-18x^3-17x^3+51x^2+11x^2-33x-2x+6=0\)
\(\Rightarrow\left(x-3\right)\left(6x^3-17x^2+11x-2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(6x^3-12x^2-5x^2+10x+x-2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(6x^2-5x+1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(3x-1\right)\left(2x-1\right)=0\)
hay \(x\in\left\{3;2;\dfrac{1}{3};\dfrac{1}{2}\right\}\)
d: \(\Leftrightarrow\left(x-1\right)^2\cdot\left(x^2+3x+1\right)=0\)
hay \(x\in\left\{1;\dfrac{-3+\sqrt{5}}{2};\dfrac{-3-\sqrt{5}}{2}\right\}\)


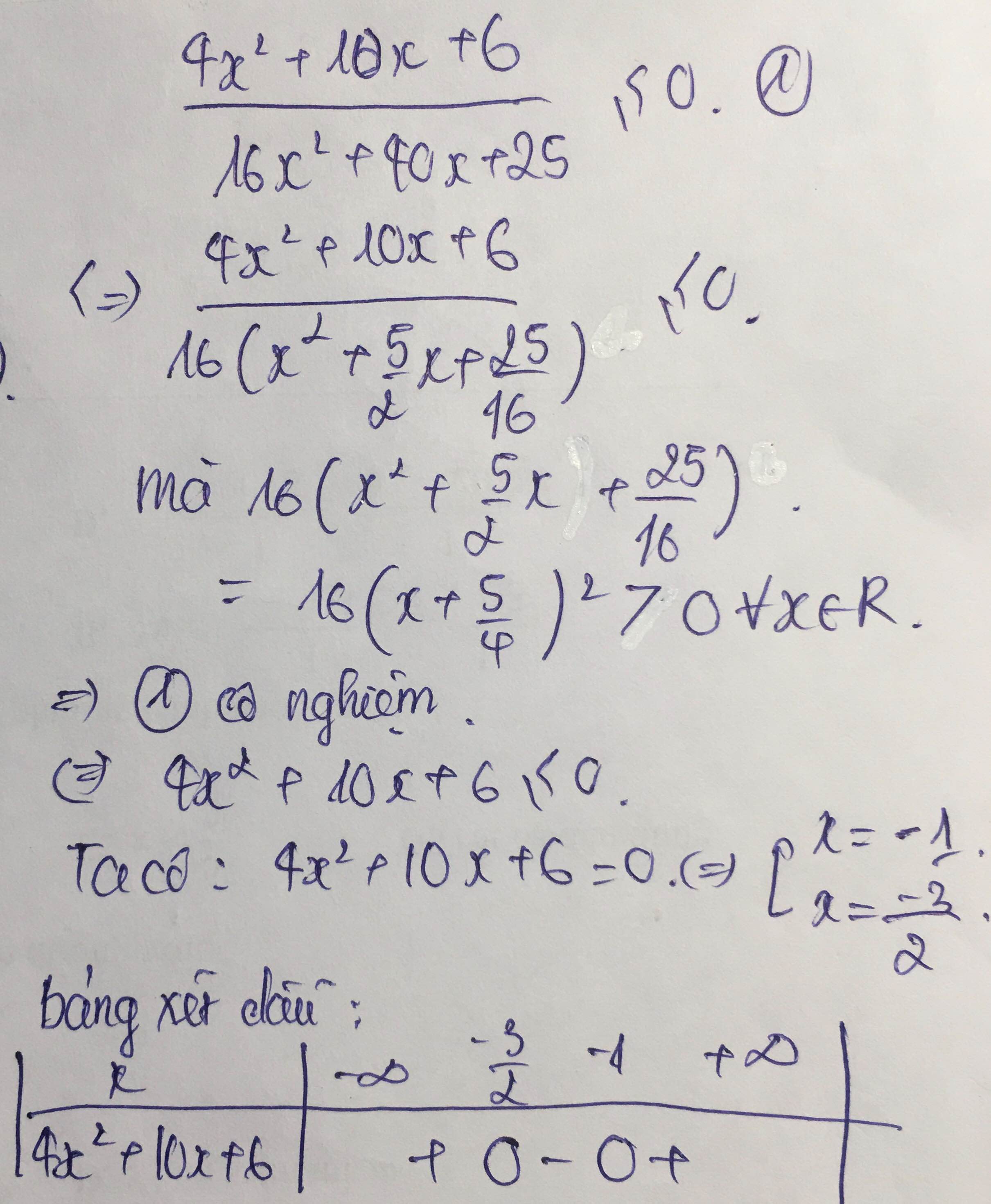

(x^2-10x+21)(x^3-x)=0
=>(x-3)(x-7)*x*(x^2-1)=0
=>x thuộc {0;1;-1;3;7}
=>B={0;1;-1;3;7}
Ta có:
\(\left(x^2-10x+21\right)\left(x^2-x\right)=0\)
\(\Leftrightarrow\left(x^2-3x-7x+21\right)x\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-7\right)x\left(x-1\right)=0\) (ĐK: \(x\in Z\))
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=3\left(tm\right)\\x=7\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
\(\Rightarrow B=\left\{1;3;7;0\right\}\)