Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Em tự giải
b. Từ giả thiết ta có \(A\left(-2;1\right)\) và \(B\left(4;4\right)\)
Gọi phương trình (d) có dạng \(y=ax+b\), do (d) qua A và B nên:
\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=2\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x+2\)
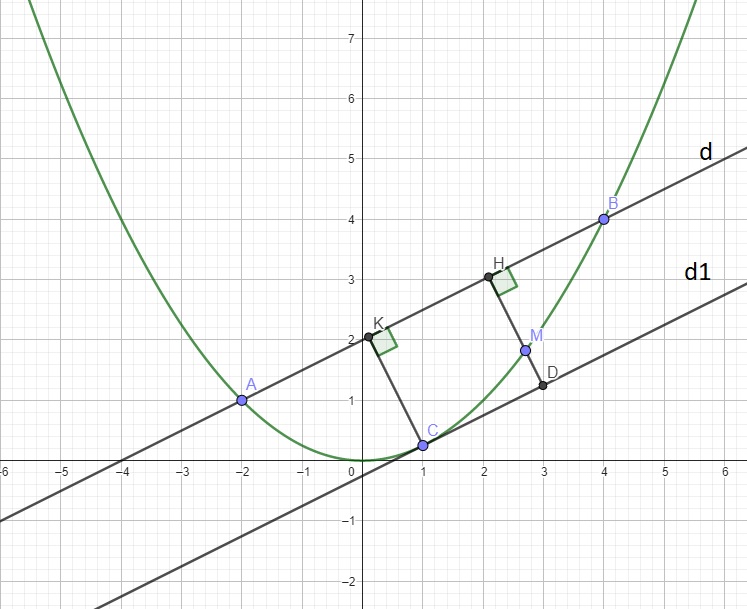
c. Câu này có vài cách giải cho lớp 9, cách nhanh nhất là sử dụng tính chất tiếp tuyến.
Từ M kẻ \(MH\perp AB\Rightarrow S_{ABM}=\dfrac{1}{2}MH.AB\)
Do AB cố định \(\Rightarrow S_{max}\) khi \(MH_{max}\)
Gọi \(d_1\) là đường thẳng song song d và tiếp xúc (P), gọi C là tiếp điểm \(d_1\) và (P)
Do \(d_1\) song song (d) nên pt có dạng: \(y=\dfrac{1}{2}x+b\)
Phương trình hoành độ giao điểm \(d_1\) và (P):
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+b\Rightarrow x^2-2x-4b=0\) (1)
Do \(d_1\) tiếp xúc (P) \(\Rightarrow\left(1\right)\) có nghiệm kép
\(\Rightarrow\Delta'=1+4b=0\Rightarrow b=-\dfrac{1}{4}\)
Thế vào (1) \(\Rightarrow x_C^2-2x_C+1=0\Rightarrow x_C=1\Rightarrow y_C=\dfrac{1}{4}\) \(\Rightarrow C\left(1;\dfrac{1}{4}\right)\)
Từ C kẻ \(CK\perp d\)
Giả sử HM kéo dài cắt \(d_1\) tại D \(\Rightarrow\) tứ giác CKHD là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông)
\(\Rightarrow CK=DH\)
Mà \(DH=MH+MD\ge MH\Rightarrow CK\ge MH\)
\(\Rightarrow MH_{max}=CK\) khi M trùng C
Hay \(M\left(1;\dfrac{1}{4}\right)\)

b) Thay x=-4 vào (P), ta được:
\(y=\dfrac{-1}{4}\cdot\left(-4\right)^2=\dfrac{-1}{4}\cdot16=-4\)
Thay x=2 vào (P), ta được:
\(y=\dfrac{-1}{4}\cdot2^2=\dfrac{-1}{4}\cdot4=-1\)
Vậy: A(-4;-4) và B(2;-1)
Gọi (d): y=ax+b(a\(\ne\)0) là phương trình đường thẳng đi qua hai điểm A và B
\(\Leftrightarrow\left\{{}\begin{matrix}-4a+b=-4\\2a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6a=-3\\2a+b=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=-1-2a=-1-2\cdot\dfrac{1}{2}=-1-1=-2\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{1}{2}x-2\)

a, - Thay tọa độ hai điểm xA, xB vào (P) ta được : \(\left\{{}\begin{matrix}y_A=2\\y_B=\dfrac{1}{2}\end{matrix}\right.\)
=> Tọa độ 2 điểm A, B lần lượt là : \(\left(2;2\right),\left(-1;\dfrac{1}{2}\right)\) .
b, - Gọi phương trình đường thẳng AB có dạng : y = ax + b .
- Thay tọa độ A, B vào phương trình ta được hệ : \(\left\{{}\begin{matrix}2a+b=2\\-a+b=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\end{matrix}\right.\)
- Thay lại a, b vào phương trình ta được : \(y=\dfrac{1}{2}x+1\)
Vậy ...
b) Với x = 4, ta có: y = x 2 /4 = 4 ⇒ A (4; 4)
Với x = 2, ta có y = x 2 /4 = 1 ⇒ B ( 2; 1)
Giả sử đường thẳng đi qua 2 điểm A, B là y = ax + b
Đường thẳng đi qua A (4; 4) nên 4 = 4a + b
Đường thẳng đi qua B (2; 1) nên : 1= 2a + b
Ta có hệ phương trình
Vậy phương trình đường thẳng đi qua 2 điểm A, B là y = 3/2 x - 2