
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>BC=10(cm)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}=5\left(cm\right)\)
c: Xét ΔABC vuông tại A có \(\widehat{ABC}=45^0\)
nên ΔABC vuông cân tại A
=>AB=AC
Hình chữ nhật ABDC có AB=AC
nên ABDC là hình vuông
Câu 2:
a: Xét tứ giác MEKH có
G là trung điểm chung của MK và EH
=>MEKH là hình bình hành
Hình bình hành MEKH có \(\widehat{MHK}=90^0\)
nên MEKH là hình chữ nhật
b: Xét ΔMHK có
N,G lần lượt là trung điểm của MH,MK
=>NG là đường trung bình của ΔMHK
=>NG//HK và NG=HK/2
NG//HK
\(D\in HK\)
Do đó: NG//HD
\(NG=\dfrac{HK}{2}\)
\(HD=\dfrac{HK}{2}\)
Do đó: NG=HD
Xét tứ giác NGDH có
NG//DH
NG=DH
Do đó: NGDH là hình bình hành
Hình bình hành NGDH có \(\widehat{NHD}=90^0\)
nên NGDH là hình chữ nhật

Bài 3:
b: Xét ΔABC có
I là trung điểm của BC
IK//AC
Do đó: K là trung điểm của AB
Xét ΔABC có
I là trung điểm của BC
IH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
K là trung điểm của AB
H là trung điểm của AC
Do đó: HK là đường trung bình của ΔABC
Suy ra: HK//BC

a) \(\dfrac{A}{x-3}=\dfrac{y-x}{3-x}\left(Đk:x\ne3\right)\)
\(A=\dfrac{\left(x-3\right)\left(y-x\right)}{3-x}=x-y\)
b) \(\dfrac{5x}{x+1}=\dfrac{Ax\left(x-1\right)}{\left(1-x\right)\left(x+1\right)}\left(Đk:x\ne\pm1\right)\)
\(A=\dfrac{5x\left(1-x\right)\left(x+1\right)}{x\left(x-1\right)\left(x+1\right)}=-5\)
c) \(\dfrac{4x^2-5x+1}{A}=\dfrac{4x-1}{x+3}\left(Đk:x\ne-3;A\ne0\right)\)
\(A=\dfrac{\left(4x^2-5x+1\right)\left(x+3\right)}{4x-1}=\dfrac{\left(x-1\right)\left(4x-1\right)\left(x+3\right)}{4x-1}\)
\(=\left(x-1\right)\left(x+3\right)=x^2+2x-3\)

a) \(A=x^4+4x+7=\left(x^2+4x+4\right)+3=\left(x+2\right)^2+3\ge3\)
\(minA=3\Leftrightarrow x=-2\)
b) \(B=x^2-x+1=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(minB=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=4x-x^2+3=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
\(maxC=7\Leftrightarrow x=2\)
d) \(D=2x-2x^2-5=-2\left(x^2-x+\dfrac{1}{4}\right)-\dfrac{9}{2}=-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{2}\le-\dfrac{9}{2}\)
\(maxD=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{1}{2}\)

chu vi hình vuông là
50x4=200cm
độ dài 1 cạnh hình vuông là
50:4=12,5cm
diện tích hình vuông là
12,5x12,5=156,25cm2

a: \(P=\dfrac{8}{x\left(x+4\right)}+\dfrac{5x}{x\left(x+4\right)}-\dfrac{2x+8}{x\left(x+4\right)}=\dfrac{8+5x-2x-8}{x\left(x+4\right)}=\dfrac{3}{x+4}\)
b: Thay x=1/2 vào P, ta được:
P=3:9/2=3x2/9=6/9=2/3
Với khác 0 ; x khác 4
\(P=\dfrac{8+5x-2x-8}{x\left(x+4\right)}=\dfrac{3x}{x\left(x+4\right)}=\dfrac{3}{x+4}\)
Thay x = 1/2 vào P ta được \(\dfrac{3}{\dfrac{1}{2}+4}=\dfrac{3}{\dfrac{9}{2}}=3:\dfrac{9}{2}=\dfrac{2}{3}\)

a)
\(=\left(\dfrac{x}{x+3}-\dfrac{x^2+9}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{3x+1}{x\left(x-3\right)}-\dfrac{1}{x}\right)\)
\(=\left(\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{x^2+9}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{3x+1}{x\left(x-3\right)}-\dfrac{x-3}{x\left(x-3\right)}\right)\)
\(=\left(\dfrac{x^2-3x-x^2-9}{\left(x+3\right)\left(x-3\right)}\right):\left(\dfrac{3x+1-x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{-3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}:\dfrac{2x+4}{x\left(x-3\right)}\)
\(=\dfrac{-3}{\left(x-3\right)}\cdot\dfrac{x\left(x-3\right)}{2x+4}\\ =\dfrac{-3x}{2x+4}\)
b)
với `x=-1/2` (tmđk) ta có
\(\dfrac{-3\cdot\left(\dfrac{-1}{2}\right)}{2\cdot\left(-\dfrac{1}{2}\right)+4}=\dfrac{1}{2}\)
c)
để P=x thì
\(\dfrac{-3x}{2x+4}=x\)
\(=>-3x=\left(2x+4\right)\cdot x\)
\(-3x=2x^2+4x\)
\(2x^2+4x+3x=0\)
\(2x^2+7x=0\)
\(x\left(2x+7\right)=0\)
\(=>\left[{}\begin{matrix}x=0\\2x+7=0\end{matrix}\right.=>\left[{}\begin{matrix}x=0\left(loại\right)\\x=-\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)
d)
mik ko bt lm=)
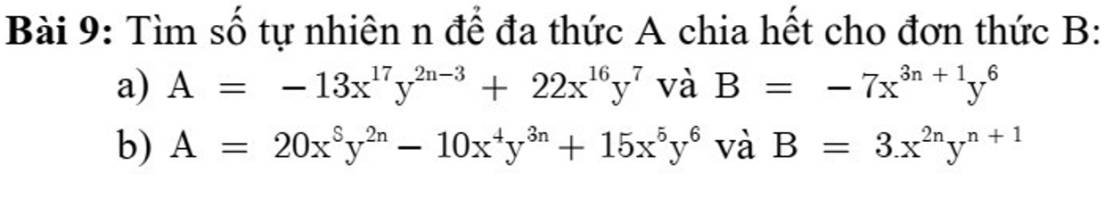

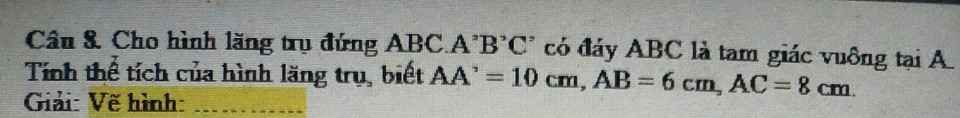

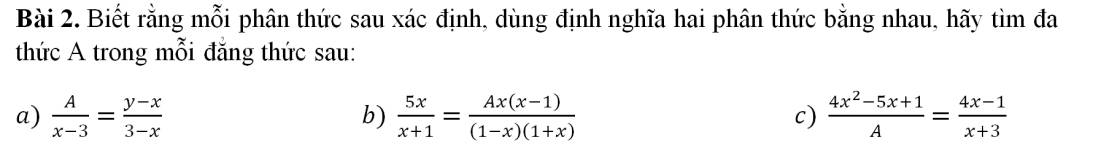 giúp em bài này với ạ ! Em cảm ơn ạ
giúp em bài này với ạ ! Em cảm ơn ạ  giúp em bài này vs ạ em cảm ơn trc ạ
giúp em bài này vs ạ em cảm ơn trc ạ
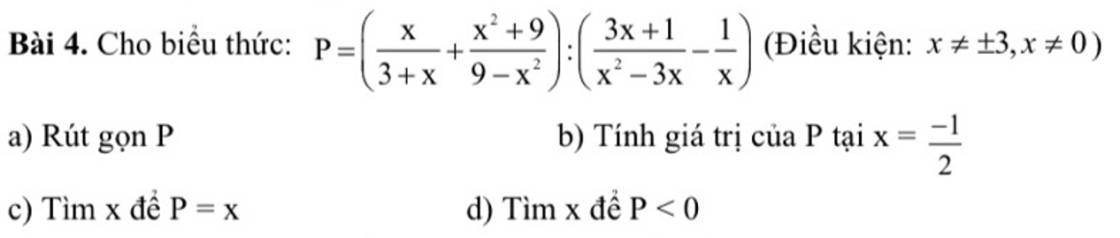

9:
a: \(\dfrac{A}{B}=\dfrac{-13x^{17}y^{2n-3}+22x^{16}y^7}{-7x^{3n+1}y^6}\)
\(=\dfrac{13x^{17}y^{2n-3}}{7x^{3n+1}y^6}-\dfrac{22x^{16}y^7}{7x^{3n+1}y^6}\)
\(=\dfrac{13}{7}x^{16-3n}y^{2n-9}-\dfrac{22}{7}x^{16-3n-1}y\)
\(=\dfrac{13}{7}x^{16-3n}y^{2n-9}-\dfrac{22}{7}x^{15-3n}y\)
Để đây là phép chia hết thì 16-3n>=0 và 15-3n>=0 và 2n-9>=0
=>n<=5 và n>=9/2
=>9/2<=n<=5
mà n là số tự nhiên
nên n=5
b:
\(\dfrac{A}{B}=\dfrac{20x^8y^{2n}-10x^4y^{3n}+15x^5y^6}{3x^{2n}y^{n+1}}\)
\(=\dfrac{20x^8y^{2n}}{3x^{2n}y^{n+1}}-\dfrac{10x^4y^{3n}}{3x^{2n}y^{n+1}}+\dfrac{15x^5y^6}{3x^{2n}y^{n+1}}\)
\(=\dfrac{20}{3}x^{8-2n}y^{2n-n-1}-\dfrac{10}{3}x^{4-2n}y^{3n-n-1}+5x^{5-2n}y^{6-n-1}\)
\(=\dfrac{20}{3}x^{8-2n}y^{n-1}-\dfrac{10}{3}x^{4-2n}y^{2n-1}+5x^{5-2n}y^{5-n}\)
Để đây là phép chia hết thì 8-2n>=0 và n-1>=0 và 4-2n>=0 và 2n-1>=0 và 5-2n>=0 và 5-n>=0
=>n<=2 và (n>=1 và n>=1/2)
=>1<=n<=2
mà n là số tự nhiên
nên n=1 hoặc n=2