
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, S= 1.2 + 2.3 + 3.4 + 4.5 + 99.100
-S= 1/1 - 1/2 + ......... + 1/4 -1/5 + [-(99.100)]
= 1/1 - 1/5 + [-(99.100)]
= 4/5 - 99/100
=-19/100
S = 19/100
Vậy S = 19/100
k mk nha
a) \(S=1.2+2.3+...+99.100\)
\(\Rightarrow3S=1.2.3+2.3.3+...+99.100.3\)
\(=1.2.3+2.3.\left(4-1\right)+...+99.100.\left(101-98\right)\)
\(=1.2.3+2.3.4-1.2.3+...+99.100.101-98.99.100\)
\(=99.100.101\)
\(=999900\)
\(\Rightarrow S=\frac{999900}{3}=333300\)

A = 1 + 2 + 3 + 4 + 5 + ... + 99 + 100
Số số hạng của dãy số đó là:
( 100 - 1 ) : 1 + 1 = 100
Tổng của dãy số đó là:
( 100 + 1 ) . 100 : 2 = 5050
=> A = 5050
\(B=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+...+\frac{1}{9900}\)
\(B=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+...+\frac{1}{99.100}\)\(B=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{99}-\frac{1}{100}\)
\(B=1-\frac{1}{100}\)
\(B=\frac{99}{100}\)

Ta có: \(A=\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}=1-\frac{1}{100}=\frac{99}{100}< 1\)
Vậy A<1
Học tốt nha!!!

\(A=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+....+\frac{1}{2^{100}}\)
\(\Rightarrow\)\(2A=2+1+\frac{1}{2}+\frac{1}{2^2}+....+\frac{1}{2^{99}}\)
\(\Rightarrow\)\(2A-A=\left(2+1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{99}}\right)-\left(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{100}}\right)\)
\(\Rightarrow\)\(A=2-\frac{1}{2^{100}}\)
\(B=1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{100}}\)
\(\Rightarrow\)\(3B=3+1+\frac{1}{3}+\frac{1}{3^2}+....+\frac{1}{3^{99}}\)
\(\Rightarrow\)\(3B-B=\left(3+1+\frac{1}{3}+...+\frac{1}{3^{99}}\right)-\left(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{100}}\right)\)
\(\Rightarrow\)\(2B=3-\frac{1}{3^{100}}\)
\(\Rightarrow\)\(B=\frac{3-\frac{1}{3^{100}}}{2}\)

\(a)\)\(\left(50-6.x\right).18=2^3.3^2.5\)
\(\Leftrightarrow\)\(\left(50-6.x\right).18=8.9.5\)
\(\Leftrightarrow\)\(\left(50-6.x\right).18=360\)
\(\Leftrightarrow\)\(\left(50-6.x\right)=360\div18\)
\(\Leftrightarrow\)\(50-6.x=20\)
\(\Leftrightarrow\)\(6.x=50-20\)
\(\Leftrightarrow\)\(6.x=30\)
\(\Leftrightarrow\)\(x=5\)
\(b)\)\(\left(x+1\right)+\left(x+2\right)+\left(x+3\right)+...+\left(x+100\right)=7450\)
\(\Leftrightarrow\)\(100x+\left(1+2+3+...+100\right)=7450\)
\(\Leftrightarrow\)\(100x+5050=7450\)
\(\Leftrightarrow\)\(100x=7450-5050\)
\(\Leftrightarrow\)\(100x=2400\)
\(\Leftrightarrow\)\(x=24\)
b.
(x+1)+(x+2)+...+(x+100)=7450
=> 100x + (1+2+3+...+100)=7450
=>100x + (100+1).50=7450
=>100x=2400
=>x=24

1b) Ta có: \(\left(1+\frac{1}{2}\right).\left(1+\frac{1}{3}\right)....\left(1+\frac{1}{100}\right)\)
\(=\frac{3}{2}.\frac{4}{3}.\frac{5}{4}......\frac{101}{100}=\frac{3.4.5....101}{2.3.4....100}=\frac{101}{2}\)
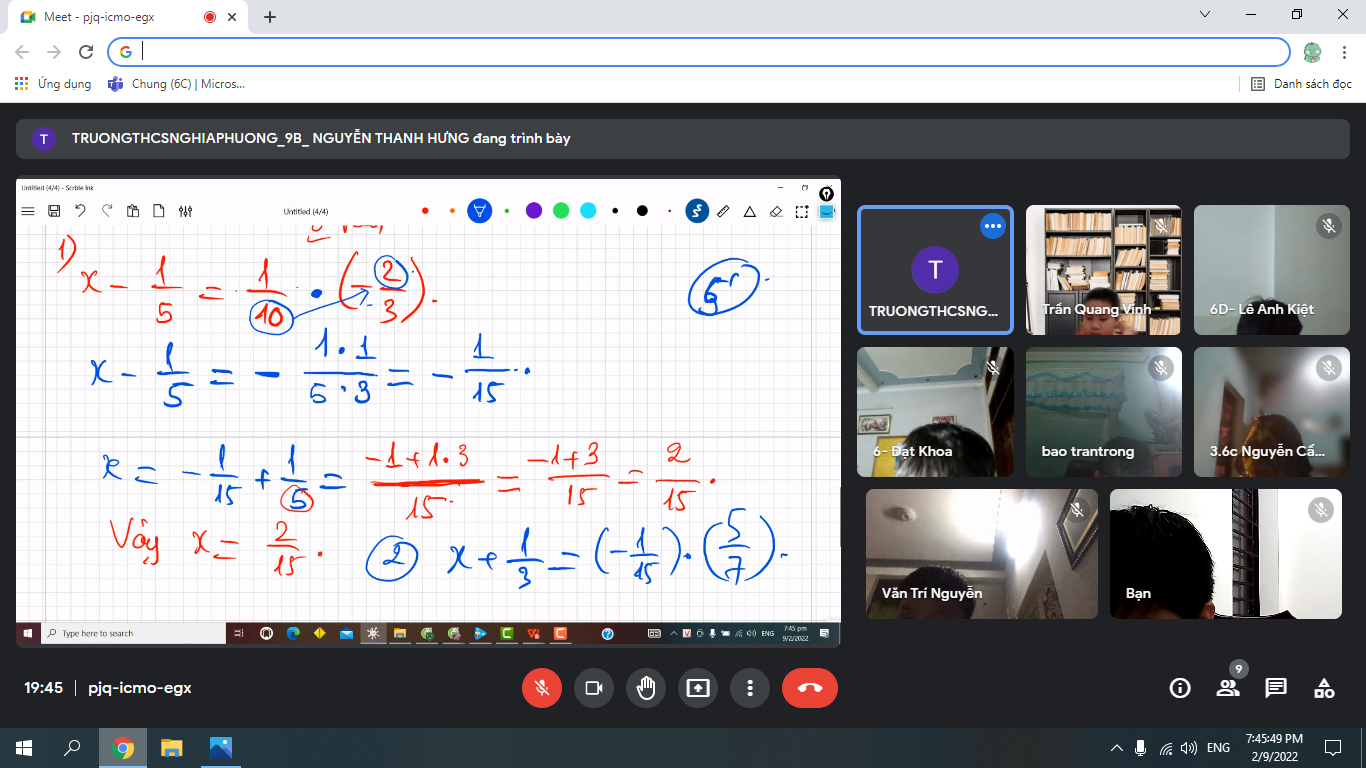 help cái bài số 2 vs
help cái bài số 2 vs
Tham khảo:Tính m=1^2+2^2+3^2 +.....+99^2+100^2 - Lê Nhật Minh